 |
Алгоритм Беллмана-Форда и его модификации
|
|
|
|
Алгоритм Беллмана-Форда является распределенным алгоритмом оптимальной маршрутизации потоков данных в ТКС. Он предназначен для вычисления оптимальных маршрутов передачи пакетов данных от данного узла-источника к остальным узлам-приёмникам ТКС с фиксированной динамикой [6,17].
Алгоритм выполняется итеративно в каждом узле ТКС. На каждой итерации алгоритма вычисляются оптимальные маршруты передачи пакетов данных от узла-источника до остальных узлов ТКС, причем число составляющих их ребер не превосходит номер итерации. Это означает, что на первом шаге алгоритма будут определяться оптимальные 1-звенные маршруты, на втором шаге – оптимальные 2-звенные маршруты, на третьем шаге – оптимальные 3-звенные маршруты и т.д.
Рассмотрим описание работы алгоритма для конкретного узла ТКС.
Введём следующие обозначения:
G(s,f,w) – ориентированный граф ТКС;
– узел-источник;
– стоимость ребра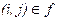 
, причём:
w(i,i) =0; 
, если узлы i и j не соединены;
, если узлы i и j соединены;
h – номер итерации, определяющий число звеньев рассматриваемых маршрутов;
Lh(j,v) – стоимость оптимального маршрута от узла j до узла v, содержащего не более h рёбер (каналов связи).
Требуется построить оптимальные маршруты от узла-источника s0 до остальных узлов ТКС и вычислить их стоимости.
Работа алгоритма:
1. Инициализация.
для всех 
;
Lh (s0, s0)=0 для всех h;
2. Итерация.
Для каждого узла вычисляем величину
. (3.2.1)
Новый маршрут до узла v получается из оптимального маршрута от узла j до узла v, на котором достигается минимум функционала 
и ребра (s0, j). При этом старый маршрут до узла v выбрасывается.
На каждой итерации для каждого узла-приемника v алгоритм сравнивает стоимости возможных (h+ 1)-звенных маршрутов от s0 до v со стоимостью маршрута, установленного в конце предыдущей итерации. Если предыдущий, более короткий маршрут (с меньшим числом ребер), имеет меньшую стоимость, он сохраняется на новой итерации. В противном случае определяется новый (h +1)-звенный маршрут от s0 до v. Этот маршрут состоит из h -звенного маршрута от s0 до некоторого узла j, определенного на предыдущей итерации, и ребра (j, v).
|
|
|
Для статических (фиксированных) ТКС с N узлами работа алгоритма заканчивается после N-1 итерации.
Для динамических ТКС с изменяющимися стоимостями (весами) каналов связи и топологией работа алгоритма ведется непрерывно.
В процессе работы алгоритма, как видно из формулы (3.2.1), на каждой итерации узлу-источнику достаточно информации о стоимостях (весах) каналов связи до его соседей и информации об оптимальных маршрутах от соседей до остальных узлов. Поэтому динамическая модификация работы алгоритма выглядит следующим образом: на каждой итерации каждый узел ТКС обменивается информацией о текущих оптимальных маршрутах со своими соседями, а также “отслеживает” изменения стоимостей (весов) исходящих из него каналов связи. После этого алгоритм пересчитывает стоимости и обновляет множество оптимальных маршрутов до остальных узлов согласно формуле (3.2.1).
Алгоритм Беллмана-Форда имеет вычислительную сложность O(N3), где N – число узлов в сети.
Алгоритм Дейкстры
Алгоритм Дейкстры используется для построения деревьев кратчайших маршрутов от узла-источника ко всем остальным узлам ТКС [3,17]. Он выполняется итеративно.
На каждой итерации алгоритм определяет кратчайший маршрут до ближайшего из необработанных ранее узлов, т.е., до узла, стоимость кратчайшего маршрута до которого не больше стоимостей кратчайших маршрутов от узла-источника до других узлов ТКС. После этого данный узел считается обработанным алгоритмом. Изначально все узлы, кроме узла-источника считаются необработанными.
|
|
|
Рассмотрим описание работы алгоритма. Введём следующие обозначения:
G(s,f,w) – ориентированный граф ТКС;
–узел-источник;
– множество узлов, обработанных алгоритмом;
(
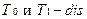)– множество узлов, обрабатываемых алгоритмом;
–остальные узлы;
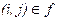– стоимость ребра , причём
w(i,j) =0; , если эти два узла не соединены непосредственно;
, если эти два узла непосредственно соединены;
L(j), где 
, – оценка алгоритмом стоимости маршрута от узла-источника s0 до узла v;
L(j), где 
, – стоимость кратчайшего маршрута от узла-источника s0 до узла v. (Для остальных j значение L(j) не определено).
Требуется построить дерево кратчайших маршрутов от узла-источника s0 до остальных узлов ТКС и вычислить их стоимости.
Работа алгоритма:
1. Инициализация.
T1 - пусто, T1 ={ s0 }, т.е. вначале множество обработанных узлов состоит только из узла-источника. Узлу-источнику сопоставляется пустой маршрут.
L (v)= w(s0vv) для 
, т.е. начальные стоимости маршрутов к соседним узлам – это веса соответствующих ребер графа G, причём L(s0)=0.
2. Шаг алгоритма.
Берем из T1 узел с минимальной оценкой стоимости маршрута, помещаем его в T0 и и обозначаем соответствующий ему маршрут как кратчайший. Иными словами,
находим 
такой, что
. (3.2.2)
При этом рассматриваем все ребра с начальным узлом x. Для каждого ребра (x, j) выполняется одно из трех действий:
А) если , то никаких действий не производится;
Б) если 
, то j переводится из множества T2 в T1, причем ей сопоставляются значение
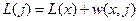, (3.2.3)
а также маршрут, состоящий из кратчайшего маршрута до x и ребра (x,j).
В) если , то производится новая оценка
, (3.2.4)
и узлу j сопоставляется соответствующий оценке маршрут (либо прежний, либо как в Б)).
Итерации повторяются до тех пор, пока T0 не станет равно s. По окончании работы алгоритма для каждого узла x будет определен кратчайший маршрут к нему от узла-источника, а значение L(x) будет соответствовать стоимости этого маршрута.
Алгоритм Дейкстры имеет вычислительную сложность O(N2), где N – число узлов ТКС.
|
|
|
