Оптимальная статическая маршрутизация в глобальных мульти-агентных ТКС

Сначала рассмотрим задачи и методы маршрутизации потоков данных в статических (фиксированных) глобальных ТКС с одним внешним агентом-пользователем (клиентом). В этом простейшем случае предполагается, что число узлов, топология и стоимость каналов связи глобальной ТКС известны и не изменяются с течением времени, а в роли клиента выступает один агент-пользователь, который через свой персональный компьютер передает сообщение или запрос в ТКС, используя один из ближайших узловых компьютеров или маршрутизаторов глобальной сети.

В общем случае глобальная ТКС состоит из автономных взаимосвязанных подсетей, каждая из которых обслуживается своим автономным (локальным) маршрутизатором. Это означает, что любой локальный маршрутизатор, зная топологию и стоимость каналов связей своей подсети и адреса принадлежавших к ней узла-источника и узла-получателя данных, способен спланировать или оптимизировать маршруты передачи пакетов данных между этими заданными начальными и конечными узлами автономной подсети.

Обычно маршрутизаторы подсетей взаимодействуют через магистральные каналы связи глобальной ТКС. Поэтому между магистрально связанными маршрутизаторами также могут быть спланированы или оптимизированы маршруты передачи пакетов данных, проходящие через несколько подсетей.

В том случае, когда узел-источник, связанный с внешним агентом-пользователем ТКС, и узел-получатель, связанный с некоторым узловым компьютером, находятся в разных подсетях глобальной ТКС, возможна "сборка" требуемого (в частности, оптимального) глобального маршрута из его фрагментов, спланированных соответствующими локальными и магистральными маршрутизаторами.

При децентрализованной маршрутизации в глобальной ТКС магистральный фрагмент маршрута, соединяющий начальный и конечный фрагменты двух связанных подсетей, планируется магистральными маршрутизаторами.

При централизованной маршрутизации для этого может быть выделен специальный глобальный маршрутизатор-координатор, иерархически связанный со всеми магистральными маршрутизаторами и знающий топологию и стоимость связей между ними.

Каждой автономной подсети глобальной ТКС соответствует ориентированный граф (графовая модель) с весами, вершины a_i которого соответствуют узлам подсети, а рёбра r_j и их веса w_j – каналам связи между узлами и стоимостям этих каналов связи. Если каналы связи являются двусторонними, то их стоимости и соответственно веса на графе могут быть различными для разных направлений передачи данных. Точно также магистральная подсеть, связывающая между собой все маршрутизаторы автономных (локальных) подсетей глобальной ТКС, может быть представлена “магистральным” графом с соответствующими весами вида

, , , . (2.6.1)

Ориентированным маршрутом в орграфе G называется чередующаяся последовательность вершин и ребер вида

, (2.6.2)

где s – начальная вершина, f – конечная вершина.

На взвешенном графе G может быть построен граф допустимых маршрутов G_p, связывающих узел-источник s с узлом-получателем f и не имеющий петель. Любой ориентированный путь на этом графе может служить маршрутом адресной передачи данных в ТКС. Однако стоимость передачи данных по разным маршрутам может быть различной.

В общем случае веса w_j на графе допустимых маршрутов могут быть функциями от числа его узлов, расстояний между ними, пропускной способности каналов связи, измеренной величины задержки передаваемых пакетов данных и т.п. В задачах стохастический маршрутизации веса w_i могут зависеть от средней загруженности каналов связи, средней длины очереди в ТКС и т.п.

Обозначим через s узел-источник данных, а через f узел-получатель данных в глобальной ТКС. Им соответствуют начальная вершина s и конечная вершина f на графе допустимых маршрутов, причём каждому ребру r_i этого графа соответствуют веса w_i = w_i(r_i), равные стоимости передачи данных по соответствующему каналу связи в заданном направлении.

Общая стоимость j -го допустимого маршрута передачи данных от узла s к узлу f глобальной ТКС определяется функционалом качества вида

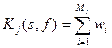, (2.6.3)

где M_j - число звеньев (рёбер графа) j -го маршрута, соединяющего граничные вершины s и f.

Оптимальным маршрутом передачи данных между заданными начальным узлом (вершиной) s н конечным узлом (вершиной) f будем называть такой маршрут, на котором функционал (2.6.3) принимает минимальное значение среди всех допустимых маршрутов, т.е.

. (2.6.4)

В общем случае, минимум (2.6.4) функционала (2.6.3) может достигаться не на одном, а на нескольких допустимых маршрутах, каждый из которых является оптимальным. В этом проявляется многозначность (многовариантность) решения задачи оптимальной глобальной маршрутизации. Эта неоднозначность полезна для равномерного распределения трафика и адаптации к перегрузкам.

В частном случае, когда требуется минимизировать общее количество передач пакетов данных между узлами s и f получим, что w_i =l и К_j= N_j. Если же вес w_i равен расстоянию между соответствующими узлами j -го маршрута, то минимизация функционала (2.6.3) приводит к определению кратчайшего маршрута (пути), соединяющего узел-источник и узел -получатель данных.

Стоимость w_i канала связи можно выбрать обратно пропорциональной скорости передачи данных по этому каналу или прямо пропорциональной задержке пакетов. В этих случаях минимизация критерия качества (2.6.3) приводит к оптимальным маршрутам с наибольшей скоростью передачи данных или минимальными задержками пакетов соответственно.

Разработчики сети ARPANET использовали для оптимальной маршрутизации критерий (2.6.3), где в качестве весов w_i использовались сначала длины очереди, а затем непосредственно измеряемое время задержки в i -том канале связи ТКС. При этом обнаружилось, что в процессе вычисления оптимальных маршрутов возникали нежелательные эффекты «пробуксовки» и «колебаний», а при передаче по этим маршрутам наблюдались канальные и сетевые перегрузки. Чтобы устранить эти недостатки, было предложено в качестве весов w_i в критерии (2.6.3) использовать величины, характеризующие степень использования i-го канала связи. В этом случае оптимальные маршруты при низкой нагрузке оказывались близки маршрутам, получаемых в случае, когда w_i является временем задержки, а при высокой нагрузке они были близки маршрутам, получаемым в случае, когда w_i обратно пропорциональны пропускной способности i-го канала связи ТКС.

Следует отметить, что во всех коммерческих ТКС стоимости каналов связи задаются независимо от реального трафика (сетевой нагрузки). Это позволяет гарантировать сходимость алгоритмов оптимальной маршрутизации в глобальных ТКС и отделить этот процесс от адаптивного управления передачей пакетов по маршруту.