Расширение карт маршрутизации и интенсивность потоков данных

Рассмотрим очень важное свойство матриц вида (4.4.2) для корректных СРКМ.

Зафиксируем узел-получатель и запустим из каждого узла в a_j поток с соответствующей интенсивностью x_i. Из (4.3.3) и (4.4.4) следует, что для того, чтобы определить, с какой интенсивностью совокупность этих потоков проходит через узлы ТКС, достаточно рассмотреть соответствующие элементы следующего вектора “интенсивностей”:

. (4.5.1)

Рассмотрим обычные РТМ и РКМ. Расширим РТМ и РКМ согласно (4.4.1) в следующем виде:

, (4.5.2)

. (4.5.3)

Назовем 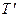расширением карты маршрутизации T. Заметим, что такое расширение РКМ не приведет к изменению в распределении информационных потоков в ТКС.

Рассмотрим узлы и зафиксируем узел-получатель . Будем говорить, что узел a_k доминирует над узлом a_i по отношению к узлу a_j (в контексте карты маршрутизации T), если при управлении потоками данных, задаваемом РКМ T, существует такая совокупность потоков данных, при которой поток данных, направленный к узлу-получателю a_j узлом a_k, будет протекать через узел a_i. Обозначим это отношение доминирования соотношением

. (4.5.4)

Заметим, что отношение доминирования не транзитивно, т.е. из соотношений

(4.5.5)

не следует, что

. (4.5.6)

В качестве примера рассмотрим граф, соответствующий некоторой ТКС, приведенный на рисунке 4.5.1. Пусть для него задана РКМ T. Рассмотрим таблицы маршрутизации из её расширения 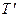для узла-получателя a₅ =f

 

Пусть эти таблицы заданы следующим образом:

 

(4.5.7)

Из (4.5.7) видно, что

и . (4.5.8)

Однако при этом

. (4.5.9)

Будем говорить, что узел a_k транзитивно доминирует над узлом a_i по отношению к узлу a_j (в контексте карты маршрутизации T), если существует последовательность узлов вида

, (4.5.10)

такая, что 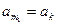, , 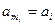и для любых 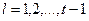справедливо соотношение

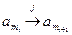. (4.5.11)

Обозначим такой тип доминирования следующим образом:

. (4.5.12)

Рассмотрим несколько свойств, связанных с отношениями доминирования и транзитивного доминирования узлов ТКС.

Лемма 4.5.1: Пусть задан орграф G(A,W,R), соответствующий некоторой ТКС, и на нем определена корректная РКМ T и её расширение 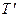. Тогда для любого узла-получателя и пары отличных от него узлов справедлива импликация вида:

если , то 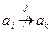. (4.5.13)

Докажем утверждение Леммы 4.5.1. Пусть доминирование узла a_k над узлом a_i проявляется при интенсивности потока x_k в a_k и x_i в a_i (будем рассматривать только этот один поток, направленный от a_k к a_j и проходящий через a_i, для которого x_i ≤ x_k. Тогда такое доминирование будет проявляться при любой интенсивности x>x_i. в узле a_i Это происходит в силу того, что всегда можно создать поток данных, направленный от a_i к a_j. Заметим, что любой поток от узла a_i к узлу-получателю a_j с интенсивностью x≥x_i не может проходить через узел a_k, поскольку в этом случае появился бы циклический маршрут, что соответствовало бы существованию бесконечного маршрута и противоречило бы условию корректности РКМ.

Теперь докажем, что любой поток от узла a_i к узлу a_j с интенсивностью x<x_i не будет проходить через узел a_k. Действительно, если это не так, то такой поток с интенсивностью меньшей, чем x_i, будет протекать через a_k с интенсивностью, не превосходящей x_i, и, следовательно, не превосходящей x_k. Тогда можно создать новый поток от a_k к a_j с такой интенсивностью, чтобы суммарная интенсивность потоков на узле a_k была равна x_k. Оба эти потока будут проходить через a_i, что приведет к появлению циклических, а, значит, бесконечных маршрутов, что противоречит условию корректности РКМ. Таким образом, поток любой интенсивности, направленный от узла a_i к узлу a_j через a_k протекать не может, и, следовательно,

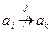. (4.5.14)

Лемма 4.5.1. доказана. Из неё вытекает следующее следствие.

Следствие 4.5.1: В условиях леммы 4.5.1 для любого узла , отличного от узла-получателя, справедливо следующее соотношение:

. (4.5.15)

Лемма 4.5.2: Пусть выполнены условия леммы 4.5.1, задан узел-получатель и существуют три узла такие, что

, а (т.е., 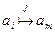). (4.5.16)

Рассмотрим потоки, направленные к узлу-получателю от узлов a_i и a_k. Пусть максимальная интенсивность таких потоков от a_k, при которой они будут протекать через узел a_m, равна x_k (если верхнего ограничения нет, то полагаем, что x_k = ∞), а минимальная положительная интенсивность, с которой проходят через a_k потоки от a_i равна x_i (если минимума нет, то в качестве значения x_i принимаем инфимум положительных значений). Тогда, следующие утверждения равносильны:

1) x_i ≤ x_k., (4.5.17)

2) . (4.5.18)

Докажем, что из первого утверждения следует второе. Из леммы 4.5.1 следует, что

и . (4.5.19)

Запустим от узла a_i поток к узлу-получателю a_j, который будет протекать через a_k с интенсивностью x_i или, если x_i =0, с любой интенсивностью меньшей, чем x_k (далее под x_i будем подразумевать эту интенсивность). Из узла a_k запустим поток к a_j с интенсивностью (x_k – x_i). Тогда интенсивность суммарного потока, протекающего через узел a_k, будет равна x_k, и этот поток будет проходить через a_m, минуя a_i и не возвращаясь в a_k, так как

и . (4.5.20)

Таким образом, справедливо второе утверждение леммы 4.5.2.

Следствие первого утверждения из второго очевидно.

Лемма 4.5.2. доказана.

Лемма 4.5.3: В условиях леммы 4.5.1 справедливо следующее утверждение: любой узел 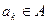, выбранный при фиксированном узле-получателе , не может транзитивно доминировать сам над собой, т.е.

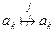. (4.5.21)

Докажем эту лемму методом от противного. Пусть существует такой узел 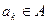, для которого имеется циклическая последовательность узлов 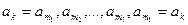, доминирующих друг над другом, т.е.

. (4.5.22)

В соответствии со следствием 4.5.1 из леммы 4.5.2 без потери общности можно считать, что элементы этой последовательности обладают следующим свойством:

 

. (4.5.23)

Рассмотрим три подряд идущих узла данной последовательности . Пусть максимальная интенсивность потоков от узла 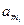к узлу-получателю, при которой он будет протекать через узел , равна (если верхнего ограничения нет, то полагаем, что ), а минимальная положительная интенсивность, с которой через узел 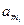проходят потоки от равна 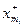(если минимума нет, то в качестве значения 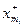принимаем инфимум положительных значений). Тогда из леммы 4.5.2 следует, что 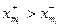. В то же время, нетрудно убедиться, что .

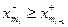Таким образом, справедлива следующая цепочка соотношений:

 

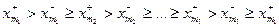. (4.5.24)

откуда следует, что . Получили противоречие, из которого следует справедливость леммы 4.4.3.

Следствие 4.5.2: В условиях леммы 4.5.1 при фиксированном узле-получателе существует отличный от него узел такой, что для любого узла 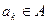, отличного от a_j и a_i, справедливо сочетание

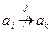. (4.5.25)

Иными словами, согласно следствию 4.5.2 для любого узла-получателя существует отличный от него узел 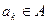такой, что при любой интенсивности x>0 справедливо уравнение

. (4.5.26)

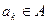Доказательство этого следствия поведем методом от противного. Предположим, что такого узла нет. Тогда существует узел-получатель такой, что для любого отличного от него узла существует узел такой, что

. (4.5.27)

Тогда можно построить последовательность вида (4.5.22) со свойством (4.5.23). Но из леммы 4.5.3 следует, что такой последовательности не существует. Поэтому сделанное предположение неверно, что доказывает справедливость следствия 4.5.2.

Следствие 4.5.3: В условиях леммы 4.5.1 при фиксированном узле-получателе справедливо следующее утверждение: если узел 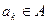транзитивно доминирует над узлом , то a_i не может доминировать над a_k, т.е.,

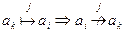. (4.5.28)

 

Утверждение следствия 4.5.3 очевидно, так как в противном случае узел a_k транзитивно доминировал бы над самим собой, что противоречит утверждению леммы 4.5.3.

Зафиксируем узел-получатель . Построим для него матрицу доминирования Q ^(j). Рассмотрим расширение РКМ T. Каждой расширенной РТМ сопоставим вектор с компонентами

(4.5.29)

Тогда матрица доминирования будет выглядеть следующим образом:

 

. (4.5.30)

 

Рассмотрим связь матрицы доминирования с отношениями доминирования узлов ТКС в форме импликации вида:

. (4.5.31)

Из соотношения (4.5.31) следует эквивалентность следующих соотношений

. (4.5.32)

Критерий корректности для РКМ можно сформулировать в виде следующей теоремы.

 

Теорема 4.5.5: Распределяющая карта маршрутизации T корректна тогда и только тогда, когда для любого узла-получателя верно, что его матрица доминирования Q ^(j) удовлетворяет следующему требованию:

(4.5.33)

Докажем сначала необходимость. Пусть РКМ корректна. Зафиксируем узел-получатель . Предположим, что существует число k такое, что

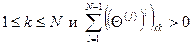. (4.5.34)

Тогда из (4.5.34) следует, что

, (4.5.35)

а это противоречит утверждению леммы 4.5.3.

Теперь докажем достаточность. Рассмотрим РКМ. Так как все прокладываемые этой картой маршруты будут заканчиваться в узле-получателе a_j, то нам остается доказать, что все определяемые РКМ маршруты будут конечнозвенными.

Предположим, что РКМ некорректна. Тогда будут существовать бесконечные маршруты, т.е., маршруты, содержащие циклы. В этом случае будут существовать узлы, транзитивно доминирующие сами над собой. Но из (4.5.33) в силу (4.5.32) следует, что для любой узел 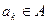не может транзитивно доминировать сам над собой, т.е.

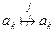. (4.5.36)

Полученное противоречие доказывает корректность РКМ и справедливость теоремы 4.5.5.

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: