 |
Нейросетевая маршрутизация в мульти-агентных ТКС
|
|
|
|
Рассмотрим нейросетевую маршрутизацию в мульти-агентных ТКС. Как известно [14,16,28,30], нейронные сети представляют собой эффективную вычислительную модель, позволяющую распознавать образы или аппроксимировать функции любой сложности, основываясь на неполной информации, заключенной в обучающей базе данных (БД).
Свойство нейронных сетей получать нужный результат при зашумленных входных параметрах чрезвычайно полезно при маршрутизации в глобальных ТКС с непредсказуемо изменяющимися топологией и сетевым трафиком.
Нейронные сети можно рассматривать как оптимизатор некоторого функционала, оценивающего стоимость прокладываемых маршрутов, что делает их неким аналогом распределительных оптимальных таблиц и карт маршрутизации, представленной на рис. 4.2.1, б).
Для решения задач маршрутизации используются в основном два вида нейронных сетей: сети перцептронного типа и сети Хопфилда. Однако решения, вычисляемые сетями перцептронного типа, как правило, неустойчивы. Поэтому ниже рассматриваются нейронные сети Хопфилда (НСХ) и их модификация.
Построим нейронную сеть для мульти-агентной модели, предложенной в 4.6.
Рассмотрим оптимизационную задачу (4.6.6)-(4.6.7). Данная задача при выполнении условий I-IV имеет, по крайней мере, одно решение. При этом для всех решений значения вектора распределения нагрузок ρ будут одними и теми же.
Достаточным условием решения оптимизационной задачи (4.6.6)-(4.6.7) с линейными ограничениями при помощи НСХ, является строгое монотонное возрастание минимизируемой функции.
Рассмотрим систему (4.6.4). Так как для конкретного множества 
значением функции ΦD является положительная константа, то её можно перенести в левую часть, не меняя условий задачи, т.е.
|
|
|
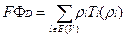. (4.7.1)
Введём матрицу Δ вида
, (4.7.2)
где δij – доля интенсивности информационного потока xj, которая приходится на ребро (канал связи) i.
Так как ρ l = ρ l (x), то задачу (4.6.6)-(4.6.7) можно переформулировать следующим образом:
FΦD → min (4.7.3)
при ограничениях
. (4.7.4)
В качестве возможных решений задачи (4.7.3), (4.7.4) будем искать векторы (ρ, x). Без потери общности можно считать, что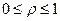 
и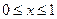 
.
Построим энергетическую функцию E = E(ρ, x) для НСХ, решающей оптимизационную задачу (4.7.3)-(4.7.4). Потребуем, чтобы функция E была квадратичной формой от (ρ, x).
Сначала рассмотрим функцию E0:
, (4.7.5)
где αij - некоторые положительные константы, причем α11 – достаточно малое число. Однако E0 не является квадратичной формой, так как в первой сумме присутствуют нелинейные элементы T l (ρ l).
Заменим первую сумму в (4.7.5) на квадрат линейной комбинации ρ. Тогда получим следующую энергетическую функцию для НСХ:
(4.7.6)
где параметры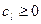 
и достаточно малы.
Важно отметить, что основным требованием при составлении энергетической функции для решения подобных оптимизационных задач с линейными ограничениями является достаточно малое значение слагаемого, соответствующего минимизируемой функции. В этом случае приближённое решение будет не слишком сильно отличалось от точного. Поэтому коэффициенты линейной комбинации берутся достаточно малыми. В то же время, нельзя задавать их слишком малыми, поскольку это замедлит сходимость процесса поиска решения оптимизационной задачи маршрутизации.
Замена (4.7.5) на (4.7.6) допустима, поскольку для двух строго возрастающих функций с одинаковыми областями определения (задаваемыми системой (4.7.4) экстремумы достигаются в одинаковых точках.
Таким образом, синтезирована модель НСХ, состоящая из |E|+|Π| нейронов, где Π - упорядоченное множество всех маршрутов для всех пар узлов, а E – множество рёбер графа, соответствующего ТКС. Эта модель НСХ ориентирована на централизованную схему мульти-агентной маршрутизации, представленной на рис. 4.2.2, а).
|
|
|
Теперь рассмотрим задачу локальной оптимизации (4.6.8) для распределённой схемы мульти-агентной маршрутизации, изображённой на рис. 4.2.2., б). При выполнении условий I-IV эта задача имеет, по крайней мере, одно решение.
Рассмотрим первое уравнение системы (4.6.8). В силу второго и четвертого неравенств системы получим, что для любого x справедливо неравенство вида
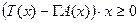. (4.7.8)
Отсюда следует, что неотрицательная функция (T(x)-Γy)x принимает нулевые значения (с учетом остальных ограничений) в точках возможных решений неравенств (4.7.8). Это означает, что точки минимумов данной функции совпадают с решениями оптимизационной задачи (4.6.8). С учетом (4.7.8) и того, что
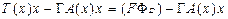, (4.7.9)
переформулируем задачу (4.7.1) следующим образом:
(4.7.10)
Эту задачу можно свести к следующей оптимизационной задаче:
(4.7.11)
Заметим, что zp=0, если
Tp(x) = (ΓA(x))p.
Поэтому с учетом неравенств xp≥0 и zp>0 получим, что
Tp(x)>(ΓA(x))p и xp=0. (4.7.12)
Построим НСХ, решающую оптимизационную задачу (4.7.11). В качестве возможных решений будем искать векторы (x, z). Так же, как и в предыдущей задаче, будем полагать, что 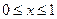и 
.
Из первого равенства в системе ограничений следует, что
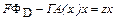. (4.7.13)
Таким образом, энергетическая функция E для НСХ будет иметь следующий вид:
(4.7.14)
Модель НСХ с энергетической функцией (4.7.14) состоит из 2|Π| нейронов, где Π - упорядоченное множество всех маршрутов для всех пар узлов ТКС. Эта нейронная сеть ориентирована на решение задачи локальной оптимизации для распределенной схемы мульти-агентной маршрутизации.
Проведенные исследования показали применимость предложенных модификаций НСХ для решения задачи мульти-агентной маршрутизации потоков данных в статических ТКС, конфигурация которых не меняется с течением времени, а также в динамических ТКС. Была исследована возможность адаптации полученных нейросетевых решений к мульти-агентным ТКС с ограниченной пропускной способностью каналов связи.
Основным недостатком предложенных моделей и метода нейросетевой маршрутизации для распределенной и централизованной схем является большой объем предварительных вычислений (прокладка всевозможных маршрутов, расчёт весов, зависящий от большого числа параметров и т.д.). Поэтому целесообразно исследовать возможность минимизации и автоматического расчета входных параметров нейронных сетей, а также произвести имитационное моделирование и программно-аппаратную реализацию нейросетевых маршрутизаторов в составе глобальных ТКС с изменяющейся динамикой.
|
|
|
Список литературы
1. Олифер В.Г., Оливер М.А. Компьютерные сети. Принципы, технологии, протоколы. - Спб.: Питер, 2001. - 672с.
2. Harshall F. Data Communication, Computer Networks and Open Systems. -Adisson - Wesly, 1996.
3. Tanenbaum A.S. Computer Networks. – Prentice Hall, 1996.
4. Хелеби С. Мак-Ферсон Д. Принципы маршрутизации в Internet. 2-е издание.: Пер. с англ. – М: Издательский дом «Вильямс», 2003. – 448 с.
5. Басанер Р., Саати Т. Конечные графы и сети. - М.: Наука, 1973. - 368 с.
6. Уолренд Дж. Телекоммуникационные и компьютерные сети. Вводный курс.- М.: Постмаркс. - 2001. - 480 с.
7. Шварц М. Сети связи: протоколы, моделирование и анализ. - М.: Наука, 1992.
8. Уолрендж Дж. Введение в теорию сетей массового обслуживания.- М.:Мир, 1993.
9. Иванов А.В. Контроль соответствия в телекоммуникациях и связи. Измерения, анализ, тестирование, мониторинг. - М.: Syrus Systems, 2000.
10. Ben-Artzi A., Chanda A., Warrier U. Network Management of TCP/IP Networks: Present and Future. - IEEE Network Magazine, 1990, pp. 35-43.
11. Varaiya P., Walrand J. High-Performance Communication Networks. - Morgan Kaufmann, 1996.
12. Кох Р., Яновский Г.Г. Эволюция и конвергенция в электросвязи. - М.: Радио и связь, 2001. - 280 с.
13. Cairncross F. The Death of Distance. - Harvard Business School Publishing, 1997. -303 с.
14. Каллан Р. Основные концепции нейронных сетей. - М.: Издательский дом «Вильямс», 2001. – 287 с.
15. Тимофеев А.В. Построение адаптивных систем управления программным движением. - Л.:Энергия, 1980, 88 с.
16. Timofeev A.V. Intelligent Control Applied to Non-Linear Systems and Neural Networks with Adaptive Architecture.- International Journal on Intelligent Control, Neurocomputing and Fuzzy Logic, 1996, pp. 1-18.
17. Столлингс В. Современные компьютерные сети. – СПб: Питер, 2003, - 783 с.
18. Boyan J., Littman M. Packet Routing in Dynamically Changing Networks: A Reinforcement Learning Approach, Web-ресурс.
19. Вишневский В.М. Теоретические основы проектирования компьютерных сетей. – М.: Техносфера, 2003. 512 с.
|
|
|
20. Бертсекас Д., Галлагер Р. Сети передачи данных: Пер. с англ.- М.: Мир. – 1989. – 544 с.
21. Вишневский В.М., Пороцкий С.М. Динамическая маршрутизация в АТМ сетях – проблемы и решения. – Автоматика и телемеханика. – 2003. - № 6.
22. Вишневский В.М., Левнер Е.В., Федотов Е.В. Математические модели исследования алгоритмов маршрутизации в сетях передачи данных. – Информационные процессы, 2001, Т.1, № 2. – с. 103-126.
23. Дэвис Д., Барбер Д., Прайс У., Соломонидес С. Вычислительные сети и сетевые протоколы: Пер. с англ. - М.: Мир,1981. – 563 с.
24. Клейнрок Л. Коммуникационные сети: Пер. с англ. – М.: Наука, 1975. – 256 с.
25. Клейнрок Л. Вычислительные системы с очередями: Пер. с англ – М.: Мир, 1979. – 600 с.
26. Ash G.R. Dynamic Routing in Telecommunications Networks. – McGraw-Hill, 1998.
27. Комашинский В.И., Смирнов Д.А. Нейронные сети и их применение в системах управления и связи. – М.: Горячая линия Телеком, 2002. – 94 с.
28. Назаров А.В., Лоскутов А.И. Нейросетевые алгоритмы прогнозирования и оптимизации систем. СПб: Наука и техника, 2003. 384 с.
29. Тимофеев А.В. Проблемы и методы адаптивного управления потоками данных в телекоммуникационных системах. – Информатизация и связь, № 1-2, 2003, с. 68–73.
30. Тимофеев А.В., Сырцев А.В. Мульти-агентная и нейросетевая маршрутизация потоков данных в телекоммуникационных сетях. – Труды 10-ой международной конференции “Knowledge–Dialogue–Solution” (16-26 июня, 2003, Варна), 2003, с. 187–190.
31. Тимофеев А.В. Модели мульти-агентного диалога и информационного управления в глобальных телекоммуникационных сетях. – Труды 10-ой международной конференции “Knowledge-Dialogue-Solution” (16-26 июня, 2003, Варна), 2003, с. 180–186.
32. Тимофеев А.В. Проблемы и методы адаптивного управления потоками данных в телекоммуникационных системах. – Материалы VIII Международной конференции “Региональная информатика-2002” (Санкт-Петербург, 26–28 ноября 2002), часть 1, с.87.
33. Тимофеев А.В., Сырцев А.В. Нейросетевые методы оптимальной маршрутизации потоков данных. – Материалы VIII Международной конференции “Региональная информатика-2002” (Санкт-Петербург, 26–28 ноября 2002), часть 1, с.87–88.
34. Вересов И.Г., Тимофеев А.В. Модели мульти-агентной обработки информации в робототехнических и информационно-поисковых системах. – Материалы VIII Международной конференции “Региональная информатика-2002” (Санкт-Петербург, 26–28 ноября 2002), часть 2, с.13.
35. Тимофеев А.В. Статистический синтез, обучение и оптимизация полиномиальных нейронных сетей. – Нейрокомпьютеры: разработка и применение, 2002, № 5–6, с. 26–33.
36. Тимофеев А.В. Синтез нейросетевых архитектур по многозначному дереву решений. – Нейрокомпьютеры: разработка и применение, 2002, № 5–6, с. 44–49.
|
|
|
37. Тимофеев А.В. Оптимальный синтез и минимизация сложности генно-нейронных сетей по генетическим базам данных. – Нейрокомпьютеры: разработка и применение, 2002, № 5–6, с. 34–39.
38. Тимофеев А.В. Функциональный анализ неисправностей динамических систем и дефектоустойчивость стабилизирующего управления. – Доклады АМАН, 2002, т.6, № 1, с. 67–71.
39. Timofeev A.V. Physical Diagnostics and Fault Relevant Feedback Control. – Proceedings International Conference “Physics and Control” (Saint-Petersburg, August, 20-23, 2003), рр. 254–259.
40. Тимофеев А.В. Методы высококачественного управления, интеллектуализации и функциональной диагностики автоматических систем. – Мехатроника, автоматизация, управление, 2003, № 2, с. 13–17.
41. Timofeev A.V. Tools for Functional Analysis of Faults and Methods of Fault-Stable Motion Control. – Nuclear Instruments and Methods in Physics Research, A502,2003, pp.515–516.
42. Cai Z., He H., Timofeev A. Navigation Control in Unknown Environment: A Survey. – Proceedings of 10-th International Conference on Integrated Navigation Systems (June 27-29, St-Petersburg), 2003, vol. 1, pp.158-166.
43. Syrtzev A.V., Timofeev A.V. Neural and Multi-Agent Routing in Telecommunicational Networks. – International Journal “Information Theories and Their Applications”, 2003, № 2.
44. Timofeev A.V. Models for Multi-Agent Dialogue and Informational Control in Global Telecommunicational Networks. – International Journal “Information Theories and Their Applications”, 2003, № 1.
45. Тимофеев А.В., Сырцев А.В. Нейросетевое распределение мульти-агентных потоков данных в глобальных компьютерных сетях. – Труды 1-ой Всероссийской конференции “Методы и средства обработки информации” (1-3 октября 2003, Москва).
46. Тимофеев А.В., Остюченко И.В. Управление информационными потоками в образовательном учреждении. – Cборник трудов Международной конференции “Смирновские чтения”, МБИ, 2002г., с. 44–46.
47. Тимофеев А.В. Динамическая диагностика функций и состояний управляемых систем.– Труды 11-ой Всероссийской конференции “Математические методы распознавания образов”(ММРО-11)(23-29 ноября 2003, Пущино), 2003.
48. Timofeev A.V., Syrtzev A.V. Neural Approach in Multi-Agent Routing for Static Telecommunication Networks. – International Journal “Information Theories and Their Applications”, 2003, № 10, pp.167–172.
49. Timofeev A.V. Polynomial Neural Networks with Self-Organizing Architecture. – International Journal on Optical Memory and Neural Networks, 2003, N 6.
50. Тимофеев А.В., Сырцев А.В. Нейросетевые методы оптимальной динамической маршрутизации потоков данных. – Труды VIII Санкт-Петербургской международной конференции “Региональная информатика-2002” (Санкт-Петербург,2002, 26-28 ноября), Изд-во СПОИСУ, 2003, с. 146-149.
51. Тимофеев А.В. Адаптивное управление и мульти-агентная навигация потоков данных в компьютерных сетях. – Труды Международной конференции “Интеллектуальные и многопроцессорные системы” (22-29 сентября, 2003, Геленджик), том 2, с. 20-23.
52. Тимофеев А.В. Архитектура и принципы построения мульти-агентных телекоммуникационных систем нового поколения. – Труды 11-ой Всероссийской научно-методической конференции “Телематика–2004” (Санкт-Петербург, 7–10 июня 2004 г.), том 1, с. 172–174.
53. Тимофеев А.В., Остюченко И.В. Мульти-агентное управление качеством в телекоммуникационных сетях. – Труды 11-ой Всероссийской научно-методической конференции “Телематика–2004” (Санкт-Петербург, 7–10 июня 2004 г.), том 1, с. 177–179.
54. Timofeev A.V. Multi-Agent Information Processing and Adaptive Control in Global Telecommunication and Computer Networks. – International Journal “Information Theories and Their Applications”, 2003, № 10, pp. 54–60.
55. Тимофеев А.В. Адаптивное управление и самоорганизация в мульти-агентных инфотелекоммуникационных сетях. – Труды международной конференции “TECH2004” (Варна, Болгария, 15-24 июня 2004)
56. Тимофеев А.В. Мульти-агентное управление и самоорганизация в глобальных инфотелекоммуникационных сетях нового поколения. – Труды научно-практической конференции “Стратегии динамического развития России: единство самоорганизации и управления” (Москва, 16–18 июня 2004)
57. A.V.Timofeev Intellectualization for Man-Machine Interface and Network Control in Multi-Agent Infotelecommunication Systems of New Generation. – Proceedings of 9-th International Conference “Speech and Computer”(20–22 September, 2004), Saint-Petersburg, Russia, pp. 694–700.
58. A.V.Timofeev. Adaptive Control and Multi– Agent Interface for Infotelecommunication Systems of New Generation. – International Journal "Information Theories & Applications" Vol.11, 2004
59. А.В.Тимофеев. Адаптивное и интеллектуальное управление в мульти-агентных инфокоммуникационных сетях. – Сборник докладов 2-ой Всероссийской научной конференции “Управление и информационные технологии” (21–24 сентября 2004 г.), Пятигорск, с. 115–118.
60. Р. Шеннон. Имитационное моделирование систем – искусство и наука. М., «Мир», 1978, 418 с.
61. G.Schollmeier, J.Charzinski, A.Kirst¨adter, C.Reichert, K.J.Schrodi, Y.Glickman, C.Winkler Improving the Resilience in IP Networks
Сведения об авторах
Тимофеев Адиль Васильевич – доктор технических наук, профессор, Заслуженный деятель науки РФ, заведующий лабораторией нейроинформатики и интеллектуального управления Санкт-Петербургского института информатики и автоматизации РАН,
1997227, Санкт-Петербург, ул. Байконурская 19, к. 1, кв. 179, тел.: (812)3944201
199178, Санкт-Петербург, 14-я линия 39, СПИИРАН, тел.: (812) 3280421, факс: (812)3284450, E-mail: tav@iias.spb.su
Cырцев Алексей Владимирович – аспирант кафедры информатики математико-механического факультета Санкт-Петербургского государственного университета,
198504, Санкт-Петербург, Старый Петергоф, ул. Ботаническая 70, к.3, кв.88, тел.: +7-905-286-90-35, E-mail:airleks@inbox.ru
|
|
|
