 |
Централизованная и распределённая маршрутизации в мульти-агентных ТКС
|
|
В качестве математической модели статической ТКС, чьи коммуникационные характеристики не изменяются с течением времени, будем рассматривать граф
, (4.6.1)
где V – множество узлов, E – упорядоченное множество направленных дуг.
Определим набор параметров, характеризующих коммуникационные возможности мульти-агентной ТКС. Рассмотрим множество всевозможных пар узлов графа G вида:
, (4.6.2)
где первый элемент пары является узлом-источником необходимых данных, а второй – узлом-получателем запрошенных данных. Остальные параметры мульти-агентной модели определены следующим образом:
D – множество пар «источник-получатель», осуществляющих передачу пакетов в данный момент времени ( 
);
Π – упорядоченное множество всех маршрутов для всех пар узлов из D (оно может быть усеченным),
Πd – множество возможных маршрутов для данной пары узлов 
;
Tl(pl) –стоимость нагрузки ρl, приходящейся на ребро (канал связи)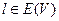 
.
На возможных маршрутах передачи данных Πd зададим матрицу инциденций вида
, где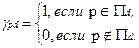 
(4.6.3)
Любая задача мульти-агентной point-to-point маршрутизации информационных потоков может быть описана конечным набором пар узлов ТКС .
Определим основные условия и параметры задачи маршрутизации следующим образом:
Φd – интенсивность информационного потока между узлами пары ;
Φ = (Φ1, Φ2, …) – вектор распределения интенсивности информационных потоков;
– общая интенсивность информационных потоков D;
xp – общая интенсивность информационного потока на маршруте 
;
x = (x1, x2, … ) – вектор распределения информационных потоков;
δlp – доля интенсивности информационного потока xp, которая приходится на дугу l;
ρl – нагрузка на ребро (канал связи) 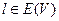, определяемая по формуле
;
ρ = (ρl, ρ2, …) – вектор распределения нагрузок на ребра (каналы связей),
Tp – средняя стоимость маршрута ,
T = (T1, T2, …) – вектор распределения стоимостей по маршрутам.
Для формализации и решения задачи оптимальной маршрутизации введем дополнительные условия:
I. Средняя стоимость маршрута определяется как сумма стоимостей нагрузок на его рёбра (каналы связей), т.е.
;
II.Для любого ребра (канала связей) 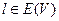справедливо
и 
;
III. Для каждого ребра (канала связей) 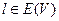, Tl(pl) выпукла и либо строго монотонно возрастает на интервале, где Tl(pl)<∞, либо Tl(pl) = const;
IV. Функция Tl(pl) непрерывна на всей области определения, причем на интервале, где Tl(pl) <∞, она непрерывно дифференцируема.
Для централизованной схемы маршрутизации с агентом-координатором решение задачи мульти-агентной маршрутизации представляет собой некоторое распределение информционных потоков, при котором общие затраты на их обслуживание минимальны.
Пусть F – общая стоимость распределения информационных потоков. Тогда
. (4.6.4)
Для любого маршрута и для любой пары узлов справедливы соотношения
. (4.6.5)
Таким образом, постановка задачи для централизованной схемы мульти-агентной маршрутизации запишется следующим образом:
F → min (4.6.6)
при следующих ограничениях:
. (4.6.7)
Для распределенной схемы мульти-агентной маршрутизации задача ставится для каждой пары отдельно. В данном случае оптимальным решением является распределение информационного потока, при котором его стоимость для каждой пары в отдельности – минимальна. Такое решение является локально- оптимальным.
Введём понятие минимального потока между парой узлов d как функцию вида
, .
Тогда решением задачи будет вектор распределения потоков x, удовлетворяющий следующим соотношениям
, (4.6.8)
где A(x) = (A1(x), A2(x), …) – вектор минимальных потоков.
Для ТКС, в которых пропускная способность каналов связи ограничена, функция Tl(pl) будет удовлетворять следующим ограничениям:
, (4.6.9)
где pmax – максимальная пропускная способность канала связи l.
В этом случае условие IV будет нарушено. Этого можно избежать, если ввести вспомогательную функцию Tl(ε)(pl) вида
(4.6.10)
где величина ε>0 и сколь угодно мала.
Лемма 4.6.1. Для Tl(ε)(pl) вида (4.6.10) выполняются условия I-IV.
Очевидно, что условия I и II будут выполнены. Докажем, что Tl(ε)(pl) непрерывно дифференцируема на [0,pmax).
Рассмотрим функцию 
. Она непрерывно дифференцируема на всей области определения и строго монотонно возрастает, причем
. (4.6.11)
Рассмотрим Tl(ε)(pl) в точке {pmax-ε}. Учитывая (4.6.9), получаем:
(4.6.12)
Из (4.6.9) следует, что в точке {pmax} функция Tl(ε)(pl) стремится к ∞, т.е. Tl(ε)(pl) непрерывна на всей области определения. С учетом (4.6.9) и (4.6.10) получаем следующее выражение для производной вспомогательной функции:
(4.6.13)
Отсюда следует, что функция Tl(ε)(pl) непрерывно дифференцируема на (0,pmax)\{pmax -ε}. Рассмотрим пределы её производной слева и справа от точки {pmax-ε}.
Так как из этого следует, что
,
то функция Tl(ε)(pl) непрерывно дифференцируема на (0,pmax). Следовательно, условие IV выполняется для вспомогательной функции (4.6.10).
Для выполнения условия III достаточно доказать, что оно выполняется на промежутке (pmax-ε, pmax). На этом интервале функция Tl(ε)(pl) как произведение двух выпуклых и положительных функций будет выпуклой и строго монотонно возрастающей.
Таким образом, лемма 4.6.1 доказана.
Отсюда следует, что, рассматриваемые для данной распределённой (децентрализованной) модели методы мульти-агентной маршрутизации применимы к ТКС с ограниченной пропускной способностью каналов связи. При этом оценочные функции стоимостей маршрутов будут строиться с некоторой погрешностью.
