|
2 Кинематический анализ сооружений
|
|
|
|
2 Кинематический анализ сооружений
2. 1 Понятие о геометрической неизменяемости
Любую расчетную систему сооружения можно представить в виде геометрически неизменяемой системы плоских тел, расположены в одной плоскости, соединенных между собой шарнирами и прикрепленных к земле при помощи опорных устройств.
Под геометрически неизменяемой системой понимается такая система соединенных между собой тел, которая не допускает взаимного перемещения ее частей без их деформаций (рис. 2. 1).
Задача кинематического анализа и состоит в том, чтобы определить геометрически изменяема или неизменяема данная система. Он проводимого в два этапа. Вначале определяется степень статической неопределимости конструкции, т. е. наличие или отсутствие лишних внешних или внутренних связей. Затем проводится собственно кинематический анализ образования (создания) конструкции, который заключается в исследовании взаимного расположения элементов конструкции (дисков) и соединяющих их связей.

2. 2 Степень свободы кинематической цепи, составленной из дисков
Степенью свободы какого-либо тела или системы называется количество независимых геометрических параметров, определяющих положение тела или системы.
|
|
Будем рассматривать плоское движение (перемещение). Если имеем движущуюся точку, то положение ее в плоской системе координат определяется двумя ее координатами х и у.
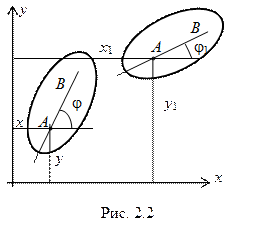
Если имеем какое-либо тело, то его положение в плоскости уже определяется тремя параметрами х у и j (рис. 21. 2), т. е. мы говорим, что тело в плоскости имеет три степени свободы W = 3.
Степень свободы может быть уменьшена какими-либо препятствиями. Всякое устройство, уничтожающее одну степень свободы будем рассматривать как одну кинематическую связь. Если одно устройство уничтожает несколько степеней свободы, то оно рассматривается как соответствующее количество кинематических связей.
|
|
|
Цилиндрический шарнир с неподвижной геометрической осью накладывает две связи. Если мы закрепим наше тело при помощи такого шарнира в точке А, то оно уже не будет иметь возможности перемещаться поступательно и его положение будет определяться только одним параметром углом j.
Расчетные схемы сооружений имеют вид кинематических цепей, состоящих из геометрически неизменяемых элементов (дисков), соединенных между собой шарнирами и прикрепленных к неподвижному элементу (земле) опорными стержнями.
Степень свободы такого сооружения можно определить следующим образом - каждый диск обладает тремя степенями свободы. Следовательно, если бы диски не были связаны между собой и с землей, то степень свободы определялась бы как 3∙ Д, где Д – число дисков. Далее, каждый шарнир, соединяющий два диска между собой, накладывает две связи и каждый опорный стержень накладывает по одной связи. Следовательно, за счет шарниров и опорных стержней степень свободы уменьшается на 2∙ Ш + С0 и будет равна
W = 3Д- 2Ш - C0, (2. 1)
где W - степень свободы; Д - число жестких дисков, из которых состоит данная конструкция; Ш - число одинарных шарниров; С0 - число опорных стержней.
Если W > 0, то данная конструкция изменяема, подвижна, т. е. является механизмом и не обеспечивает восприятие заданной на нее нагрузки, если W = 0 или W < 0, то такая конструкция может быть неизменяемой. В последнем случае, когда степень свободы W отрицательна, заданная система имеет лишние связи и является статически неопределимой.
Если рассматривается система не связанная с землей, так называемая свободная система, то ее степень свободы может быть определена как
|
|
|
W = 3Д- 2Ш - 3. (2. 2)
Количество лишних связей системы определяется количеством степеней свободы W с обратным знаком.
Под одинарным шарниром понимается шарнир, соединяющий два элемента (диска) в данной конструкции. Если шарнир соединяет одновременно три диска, то он называется двойным, т. е. выполняет функции двух одинарных шарниров, и т. д.
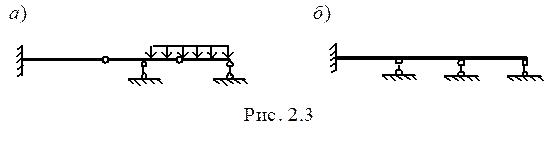
Определим степень свободы многопролетной балки (рис. 2. 3, а), которая образована из трех простых балок, соединенных двумя одинарными шарнирами и имеющей 5 опорных связей:
W = 3D - 2Ш – С0 = 3× 3 - 2× 2 - 5 = 9 – 9 = 0.
Многопролетная балка (рис. 1. 3, б) образована из одной протяженной балки с шестью опорными связями. Подсчитаем ее степень свободы:
W = 3D - 2Ш - С0 = 3× 1 - 2× 0 - 6 = - 3.
То есть, эта многопролетная неразрезная балка трижды статически неопределима или, другими словами, имеет три лишние связи.
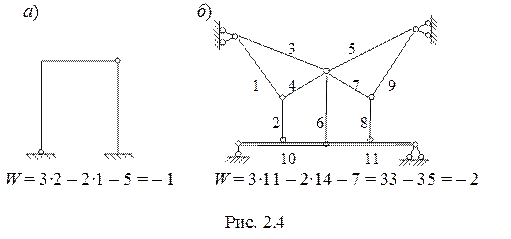
Рама, показанная на рисунке 2. 4, а состоит из двух дисков, одного одинарного шарнира и пяти опорных связей (3 в защемлении и 2 в шарнирной неподвижной опоре). Степень свободы ее W = -1 (имеет одну лишнюю связь). Комбинированная система, показанная на рис. 2. 4, б имеет две лишних связи.
|
|
|