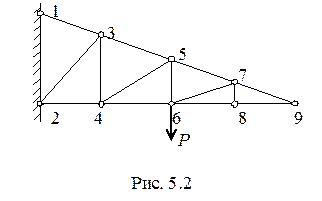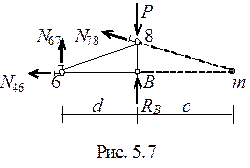|
5. Статически определимые фермы
|
|
|
|
5. Статически определимые фермы
5. 1 Классификация ферм
Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирными. При этом нагрузка к ферме прилагается в узлах, а в стержнях возникают только продольные усилия N.
Ферма, как правило, состоит из нескольких однотипных элементов ¾ панелей, при этом стержни фермы имеют свои названия (рис. 5. 1):

Фермы классифицируются по следующим признакам:
1. 1. По типу решетки: 
1. 2. По очертанию:



1. 3. По типу опирания: балочные, консольные, консольно-балочные;
1. 4. По назначению: стропильные, башенные, крановые, мостовые с ездой понизу и поверху, и др.
5. 2 Расчет простейших ферм на неподвижную нагрузку
Фермы, образованные из шарнирных треугольников последовательным присоединением узлов, называются простейшими. Они статически определимы и геометрически неизменяемы.
В задачах расчета статически определимых ферм в полной мере приходится использовать уравнения равновесия как сходящейся системы сил (при рассмотрении равновесия узла), так и произвольной системы сил. Необходимо отметить, что все методы определения усилий в стержнях фермы реализуют основной метод механики деформируемого твердого тела - метод сечений. Принято различать три основных способа определения усилий в стержнях ферм:
1) метод моментной точки используется, когда в поперечном сечении оказывается не более трех неизвестных усилий в стержнях; при этом два из них пересекаются в точке, положение которой легко определить. В сумму моментов всех сил, приложенных к рассматриваемой части фермы относительно этой точки, которая называется моментной, войдет только одно неизвестное, которое из этого уравнения и будет найдено;
|
|
|
2) метод проекций. В этом случае записывают сумму проекций всех сил, приложенных к рассматриваемой части фермы на ось х или у или другую произвольно ориентированную ось. Ось проекции выбирается так, чтобы в уравнение равновесия входило одно неизвестное усилие;
3) метод вырезания узлов применяется для определения усилий, когда в узле сходится не более двух стержней с неизвестными усилиями.
|
|
Пример 5. 1. Определить нулевые стержни заданной консольной фермы (рис. 2. 2). Вырежем узел 9 и рассмотрим его равновесие (рис. 5. 3). Узел не нагружен, и в нем сходятся два стержня.
Из уравнения равновесия
Sy = 0 получим:
N97sina = 0, откуда N97 = 0.
Запишем второе уравнение равновесия:
Sx = 0, - N97cosa - N98 = 0, тогда N98 = 0.
Таким образом, оба усилия, сходящиеся в двухстержневом ненагруженном узле, нулевые.

Рассмотрим равновесие 8-го узла (рис. 5. 4). Это так называемый трехстержневой узел с единственно выходящим стержнем. Им является стержень 8–7. Записав сумму проекций Sy = 0, нетрудно убедиться, что стержень 8–7 — нулевой, а из уравнения Sх = 0 следует, что N98 = N86.
Мысленно вырежем узел 7. С учетом того, что стержень 7–8 нулевой, 7-й узел можно рассматривать как трехстержневой с единственно выходящим стержнем 7–6, который тоже будет нулевым. Остальные узлы либо нагружены, либо не могут рассматриваться как трехстержневые, и в остальных стержнях решетки будут возникать продольные усилия.
Пример 5. 2 Вычислить усилия в отмеченных стержнях фермы (рис. 5. 5).
Наметим путь решения задачи. Усилие в стержне 3–4 удобно искать, рассмотрев равновесие узла 3; усилие в стержне 5–6 проще найти методом вырезания узла 6, а усилие в раскосе 4–5 удобнее находить, используя метод проекций. Для этого необходимо найти реакции опор и провести сечение I–I.
|
|
|
Sm1 = 0. P∙ 6–Rпр∙ 12 = 0, Rпр = Rл = Р/2.
Для определения усилия в стержне 3–5 можно воспользоваться методом моментной точки, которая находится в месте пересечения двух других усилий, оказавшихся в сечении I–I. Моментной точкой для N35 служит узел 4 (рис. 2. 5, б).

Дальнейшее решение задачи предлагается провести студентам самостоятельно. Вырезав узел 3, получим N34 = 0; вырезав узел 6, нетрудно убедиться, что стойка 5–6 сжата усилием P (N56 = - Р), а спроектировав все силы, приложенные к левой или правой частям фермы на вертикальную ось, получим усилие в раскосе N54 = Rл/cosa = 0, 5P/0, 8 = = 0, 625P. Записав уравнение моментов для левой части фермы относительно узла 4, найдем N35 = Rл3/4 = 0, 375Р.
Пример 5. 3. Определить усилия в стержнях третьей панели заданной фермы (рис. 5. 6, а). При расчетах принять:
d = 3, 6 м, h = 3 м, h1 = 0, 4h = 1, 2 м и Р = 80 кН.
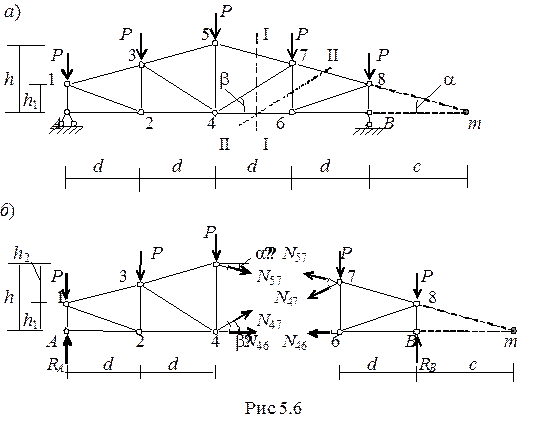
Итак, нам необходимо определить усилия в пяти стержнях фермы: в стержнях верхнего и нижнего пояса 5–7 и 4–6, в раскосе 4–7, в левой 4–5 и правой 6–7 стойках третьей панели.
Предварительно вычислим ряд геометрических параметров заданной фермы, обозначив размер h - h1 = h2.


cosa = d/l57 = 3, 6/3, 71 = 0, 97, sina = (h2/2)/l57 = 0, 9/3, 71 = 0, 242;
tga = 0, 9/3, 6 = 0, 25; с = h1/tga = 1, 2/0, 25 = 4, 8 м;
cosb = d/l47 = 3, 6/4, 17 = 0, 863;
sinb = (h1 + h2/2)/l47 = 2, 1/4, 17 = 0, 504.
1. Определяем опорные реакции.
SmA = 0. - P∙ d - P∙ 2d - P∙ 3d - P∙ 4d + RВ∙ 4d = 0; RВ = 200 кН.
В силу симметрии RА = RВ = 200 кН.
2. Для определения усилий в стержнях 4-6, 4-7 и 5-7 разрежем третью панель сечением I-I и рассмотрим равновесие одной из частей фермы под действием внешних и внутренних сил (рис. 5. 6, б). Рассматривая правую часть фермы, видим, что для определения N46 удобно записать уравнение моментов относительно моментной точки 7 (узла 7), в которой пересекаются два других неизвестных усилия N47 и N57.
Sm7=0. - P∙ d + Rb∙ d - N46(h1+h2/2) = 0.
N46 = (- 80× 3, 6 + 200× 3, 6)/2, 1 = 206 кН.
Усилие N46 направлено на чертеже от узла и получилось положительным, следовательно, стержень 4-6 растянут.
Для определения усилия N57 также удобно использовать метод моментной точки (узел 4). Рассмотрим равновесие левой части фермы.
Sm4 = 0. – Rа∙ 2d + P∙ 2d + P∙ d - (N57cosa)h = 0.
N57 = (- 200∙ 7, 2 + 80∙ 7, 2 + 80∙ 3, 6)/(0, 97× 3) = - 198 кН.
Знак «-» у усилия N57 говорит, что стержень 5-7 сжат.
|
|
|
Усилие N47 можно найти либо методом проекций на ось у всех сил, приложенных к одной из частей фермы, либо методом моментной точки. В данном случае это будет точка m, лежащая справа от опоры В (рис. 2. 6). Воспользуемся методом проекций, рассмотрев равновесие левой части фермы (рис. 2. 6, б).
Sy = 0. RА - P - P - P - N57sina + N47sinb = 0.
N47 = [- 200 + 80 + 80 + 80 + (- 198) ∙ 0, 242]/0, 504 = - 15, 7 кН
(стержень сжат).
|
|
Для вычисления усилия в стержне 6-7 проведем сечение II-II (рис. 5. 6, а) и рассмотрим равновесие правой части фермы (рис. 5. 7). Воспользуемся методом моментной точки: для усилия N67 моментной точкой будет точка m, в которой пересекаются два других усилия N46 и N78.
Smm = 0, - N67(d + c) + Pc - Rbc = 0.
N67 = (80∙ 4, 8 - 200∙ 4, 8)/8, 4 = - 69 кН,
(стержень 6-7 сжат).
|
|
В стойке 5-6 усилие будем определять методом вырезания узлов, вырезав узел 5 (рис. 5. 8). Спроецируем все усилия, сходящиеся в узле, на ось у. В силу симметрии фермы и внешней нагрузки усилие в стержне 3-5 примем равным усилию в стержне 5-7.
Sy = 0. - P - N45 - N57sina - N35sina = 0;
N45 = - 80 -2(-198) ∙ 0, 242 = 15, 8 кН, cтойка 4 - 5 растянута.
Для проверки полученных усилий можно записать уравнение проекций всех сил, приложенных к левой или правой частям фермы (рис. 5. 6, б) на ось х.
Sx = 0. N57cosa + N47cosb + N46 = 0;
(- 198) ∙ 0, 97 + (-15, 7) ∙ 0, 863 + 206 = - 205, 6 + 206 = 0.
Погрешность d, полученная в результате проверки, равна:
d = (206 - 205, 6) ∙ 100%/205, 6 = 0, 2%,
при допустимой (разрешенной) для данного типа задач 3-5%.
|
|
|