Построение линий влияния внутренних усилий.

Построение линий влияния внутренних усилий.

Построение линий влияния поперечной силы Q_c.

Пусть единичная сила находится справа от сечения «с» (рис. 3. 5). Тогда, рассматривая левую от сечения часть балки, можем записать Q_c = R_a, или

л. в. Q_c = л. в. R_a,                                       (3. 3)

получили уравнение правой ветви л. в. Q_c, то есть, когда Р = 1 перемещается по балке на отрезке с - В линия влияния поперечной силы повторяет линию влияния реакции R_А.

Теперь Р = 1 перемещается слева от сечения «с». Рассмотрим правую часть балки. Q_c = - R_в, или          

 

л. в. Q_c =( - 1)л. в. R_В.                                   (3. 4)

Получили уравнение левой ветви. В соответствии с полученными уравнениями (3. 3) и (3. 4) строим линию влияния Q_c (рис. 3. 5).

Для построения линии влияния изгибающего момента в сечении «С» используем ту же методику, что и при построении л. в. Q_c.

Пусть Р = 1 перемещается справа от сечения «С». Рассмотрим левую часть балки.

М_c = R_a∙ а, или можем записать:

 

л. в. М_c = (л. в. R_a) ∙ а,       (3. 5)

Таким образом, правая ветвь линии влияния повторяет линию влияния R_a, с множителем «а» (рис. 3. 5).

Теперь Р = 1 перемещается слева от сечения «С». Рассмотрим правую часть балки. М_c = R_В∙ b, или:

л. в. М_c = (л. в. R_B) ∙ b.                                       (3. 6)

 

При х = 0 R_В = 0, М_c = 0, при х = а   М_c = (л. в. R_B) ∙ b = (х/l)∙ b = a∙ b/l.             

Линия влияния М_c приведена на рис. 3. 5.

Отметим, что при построении линий влияния положительные ординаты откладывают выше оси ординат. Линии влияния реакций и поперечных сил безразмерны, поскольку величина единичной силы безразмерна, линии влияния моментов имеют размерность «метр».

3. 3 Линии влияния для консольной балки

 

Построение линии влияния реакции R_a

Из уравнения равновесия S y = 0,  получим  R_a = P = 1, т. е.

л. в. R_B = 1 (см. рис. 3. 6 (б)).

Построение линии влияния поперечной силы в сечении «k» Q_k.

Единичная сила Р = 1 находится справа от сечения «k». Рассмотрим правую часть балки.

Q_k = P = 1.

Далее, Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки.

Q_k = 0.

Построение линии влияния изгибающего момента в сечении «k» М_k.

Пусть Р = 1 справа от сечения «k». Рассмотрим правую часть балки.

М_k = P∙ х.

При х = 0,  М_k = 0, при х = а, М_k = 1∙ а = а.

Теперь Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки.

М_k = 0.

 

Линии влияния Q_k и М_k приведены на рис. 3. 6 (в, г).

 

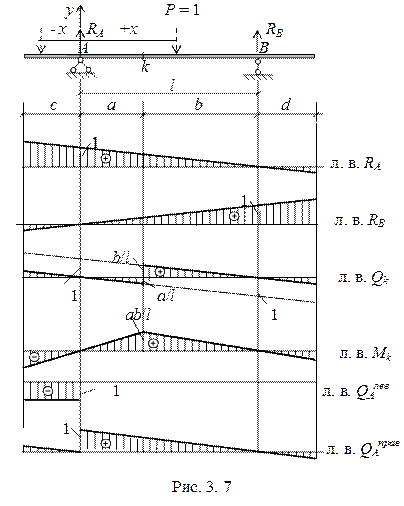
Пример 3. 1. Построить линии влияния реакций и Q_k и М_k в шарнирно опертой балке с консолями (рис. 3. 7. ). Если выбрать начало координат на левой опоре в точке А, то полученные выше выражения для линий влияния в простой балке справедливы и в данном случае. При этом, координата х будет меняться от – с до l + d.

Дополнительно необходимо построить линии влияния поперечной силы для двух соседних сечений – одно слева от опоры А, другое справа от той же опоры.

3. 4 Построение линий влияния при узловой передаче нагрузки.

Часто нагрузка передается на конструкцию не непосредственно, а через систему статически определимых балок (настилов) (рис. 3. 8). Когда единичный груз находится в начале (т m) или в конце балки (т.  n) то он полностью передается на основную конструкцию и вызывает усилия или y_m или y_n.

При движении единичной силы внутри вспомогательной балки ее действие на конструкцию осуществляется через опорные реакции R_m и R_n. Общее влияние в этом случае можно записать как:

Z_k = R_m∙ y_m + R_n∙ y_n.

В свою очередь сами реакции равны (они определяются как в обычной балке)

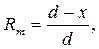
 Тогда

 -

получили уравнение прямой. При х = 0  Z_k = y_m, при x = d Z_k = y_n. Прямая, соединяющая ординаты y_m и y_n называется передаточная прямая.

В качестве примера на рис. 3. 9 показаны линии влияния при узловой передаче нагрузки в пролетном строении моста.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: