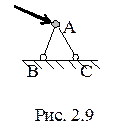2,3 Степень свободы шарнирно-стержневой плоской системы

2, 3 Степень свободы шарнирно-стержневой плоской системы

Для шарнирно-стержневых систем применима и другая формула для определения степени свободы.

Шарниры, соединяющие звенья такой системы (рис. 2. 5), можно рассматривать как точки (узлы), имеющие по две степени свободы каждая. Следовательно, суммарная степень свободы равна 2∙ У. Шарниры, соединены стержнями,  которые накладывают каждый по одной связи, т. к. они сохраняют постоянное расстояние между ними. Полное число связей будет 2∙ У - С.

Получаем следующую формулу:

 

W = 2∙ У – С - Со,                                     (2. 3)

 

Здесь: У - число узлов фермы; С - число стержней фермы; С₀ - число опорных связей.

Для свободной системы

W = 2∙ У – С – 3.                                        (2. 4)

 

В качестве примера предлагается определим степень свободы стержневых систем, представленных на рисунке 2. 6.

 

 

 

 

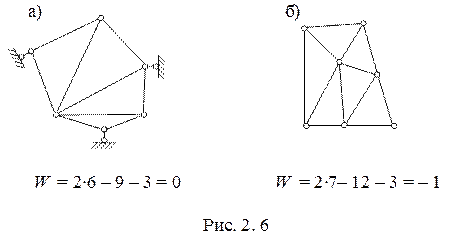
2. 4 Принципы образования геометрически неизменяемых

плоских систем

 

Условие W ≤ 0 не является достаточным признаком того, что система геометрически неизменяема. Это только необходимое условие, поскольку при W ≤ 0 система может быть изменяемой (рис. 2. 7, рис. 2. 8).

 

 

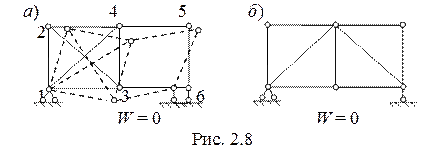
Проведем кинематический анализ простейшей фермы (рис. 2. 8, а), имеющей, как и простая балка, три связи с землей. Цифрами обозначены узлы фермы.

1. Определяем степень свободы

W = 2У - C - C₀ = 2× 6 - 9 - 3 = 0,

т. е. данная ферма не имеет лишних связей (стержней) и может быть неизменяемой.

2. Анализируя расположение стержней в предложенной стержневой системе, видим, что левая панель, образующая жесткий диск, а правая часть данной фермы представляет собой изменяемый шарнирный четырехугольник. То есть предложенная схема стержневой конструкции изменяема. Если перенести один из стержней из левой части в правую (рис. 2. 8, б), то степень свободы не изменится, а получившаяся конструкция будет геометрически неизменяемой, поскольку она состоит из шарнирных треугольников.

Очевидно, что подсчета степени свободы недостаточно. Он должен быть дополнен анализом геометрической структуры сооружения. Этот анализ состоит из рассмотрения расположения связей системы, в установлении порядка сочетания элементов. Рассмотрим простейшие законы образования геометрически неизменяемых систем.

 1. Узел (материальную точку) можно присоединить к другому телу (земле) для создания геометрически неизменяемой системы при помощи двух стержней (рис. 1. 9). При этом шарниры А, В и С не должны лежать на одной прямой.

 

 

2. Два диска можно соединить в неподвижную конструкцию либо при помощи трех стержней (рис. 2. 10, а), которые не должны быть параллель­ны друг другу и не пересекаться в одной точке, либо при помощи одного шарнира и одного стержня (рис. 1. 10, б) (стержень и шарнир не должны лежать на одной прямой). В данном случае наглядно видно, что шарнир заменил две связи. В дальнейшем это качество одинарного шарнира будет использовано.

 

3. Три диска наиболее просто можно объединить в геометрически неизменяемую конструкцию при помощи трех шарниров (рис 2. 11). При этом шарниры не должны лежать на одной прямой, в противном случае будем иметь мгновенно изменяемую конструкцию. На рис. 2. 9, 2. 10, б, и 2. 11 показаны так называемые шарнирные треугольники, которые являются простейшей неизменяемой конструкцией и используются при создании более сложных конструкций.

4. К двум дискам, соединенным шарниром, можно прикрепить узел при помощи трех стержней. При этом шарниры А, В и С не должны принадлежать одному диску (рис. 2. 12).

 

Как было указано выше, система может оказаться в положении так называемой мгновенной изменяемости, когда основные соединяющие шарниры находятся на одной прямой, либо опорные (связующие) стержни параллельны друг другу.

На рис. 2. 13, а приведена дважды статически неопределимая ферма, которая является мгновенно изменяемой, поскольку опорные стержни параллельны. На рис. 2. 13, б представлена статически определимая конструкция, состоящая из двух ломаных стержней. Если ломаные стержни представить как диски и в качестве третьего диска использовать опорное устройство (землю), то получим пример соединения трех дисков тремя шарнирами, лежащими на одной прямой. Это мгновенно изменяемая система, в которой невозможно найти опорные реакции. Если же изменить один из размеров одного ломаного стержня, шарниры не будут лежать на одно прямой и задача может быть решена.

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: