 |
6.2.3 Построение линии влияния поперечной силы.
|
|
|
|
6. 2. 3 Построение линии влияния поперечной силы.
Воспользуемся выражением (6. 3) для поперечной силы в арке
Qк = Qкб cosjк– Н sinjк.
Поскольку для заданного сечения величины cosjк и sinjк постоянны, справедливо следующее утверждение
л. в. Qк = (л. в. Qкб )cosjк – (л. в. Н) sinjк.
То есть для построения линию влияния поперечной силы в арке можно воспользоваться методом наложения линий влияния Qкб и Н, умноженных на значения соответствующих тригонометрических функций. Поступаем следующим образом (рис. 6. 10).
1. Строим линию влияния Qкбcosjк для сечения «к».
|
|
2. Вверх от оси откладываем ординаты линии влияния Н sinjк, которые получаем по левой ветви, ордината которой на правой опоре равна (l2/f) sinjк.
3. Отмечаем (штрихуем) ординаты, соответствующие выражению (6. 3).
Отметим, что в пересечении левой ветви л. в. Н sinjк с правой ветвью л. в. Qкбcosjк находится нулевая точка F1′, положение которой можно установить графически по чертежу арки. Действительно, если сила Р = 1 находится между точками к и С, то слева от точки «к» будет действовать только реакция А и для того, чтобы в сечении «к» выполнялось условие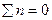 
, реакция должна быть параллельна касательной к оси арки в сечении «к».
В то же время, линия действия реакции В будет направлена вдоль прямой ВС. На пересечении этих прямых находится нулевая точка F1.
Для построения линии влияния поперечной силы в арке методом нулевой точки достаточно в сечении «к» провести касательную к оси арки направить реакцию А по этой касательной до пересечения с прямой, соединяющей шарниры С и В и получить положение нулевой точки. Далее, отложить на левой опорной вертикали ординату cosjк и провести 1-ю правую ветвь через точку F1′. Проводя вертикаль через шарнир С получаем границу 1-й и 2-й правых ветвей. Затем проводим левую ветвь, которая параллельна 1-й правой ветви (рис. 6. 10).
|
|
|
Положение нулевой точки F1 можно определить аналитически
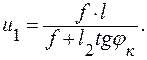(6. 10)
6. 2. 4 Построение линии влияния продольной силы.
По аналогии с построением линии влияния поперечной силы, для построения линии влияния продольной силы можно применить метод наложения и метод нулевой точки.
Для метода наложения необходимо воспользоваться выражением (6. 4) для продольной силы в арке
Nк = – Qкб sinjк – Н cosjк,
тогда:
л. в. Nк = (л. в. Qкб )sinjк + (л. в. Н) cosjк.
Здесь мы учли, что сжимающая сила в арке считается положительной.
Воспользуемся методом наложения (рис. 6. 11).
1. Строим линию влияния Qкб sinjк.
2. От оси вниз строим линию влияния Н cosjк по левой ветви (пунктирная линия).
3. Складываем ординаты построенных линий влияния.
Если продолжить правую ветвь (л. в. Н) cosjк и левую ветвь (л. в. Qкб ) sinjк получим точку F2′. Если предположить наличие консоли – ответвления от участка арки кС, по которой перемещается единичная сила, то слева отсечения «к» действует только реакция А. Если она направлена вдоль оси n, то Nк = 0, т. е.
нулевая точка находится на пересечении прямых ВС и линии действия реакции А.
Для построения лини влияния Nк методом нулевой точки достаточно найти положение т. F2′, затем отложить от левой опоры ординату sinjк и соединить полученные точки до координаты шарнира С – получим 1-ю правую ветвь. Далее строим 2-ю правую ветвь, проводя прямую от конца 1-й правой ветви до правой опоры. Левая ветвь параллельна 1-й правой ветви.
Координата нулевой точки лини влияния Nк равна
(6. 11)
Пример 6. 3 Построить линии влияния опорных реакций и внутренних усилий в сечении «к» для арки параболического очертания. Размеры арки указаны на чертеже.
|
|
|
Построение линий влияния опорных реакций RA, RB и распора H однотипно для трехшарнирных систем, так как не зависит от очертания арки (рис. 6. 12).
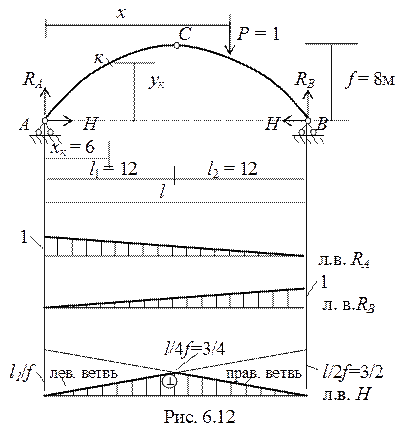
Для построения линий влияния внутренних усилий вычислим координаты сечения «к» и тригонометрические функции угла φ к.
yk = 
φ k = 33, 6°, sinφ k = 0. 554, cosφ k = 0. 836.
Построение указанных линий влияния проведем методом нулевой точки (рис. 6. 13).
Пример 6. 4. Построить линии влияния внутренних усилий в сечениях «к» и «д» в трехшарнирной раме. Размеры рамы указаны на чертеже (рис. 6. 14).
Для построения линий влияния внутренних усилий вычислим координаты сечений «к» и «d» и тригонометрические функции углов φ к и φ d.
xk = 3 м, xd = 6 м.
φ k = 45°, sinφ k = 0. 707, cosφ k = 0. 707,.
φ d(л) = 45°, sinφ d(л) = 0. 707, cosφ d(л) = 0. 707.
φ d(пр) = 0°, sinφ d(пр) = 0, cosφ d(пр) = 1.
Построение указанных линий влияния проводим методом нулевой точки (рис. 6. 14, 6. 15). Линии влияния Qd(пр) и Nd(пр) построены методом наложения.
|
|
|
