 |
Задание к практическому занятию
|
|
|
|
Кафедра экономики
Финансовый менеджмент
Методические указания к практическим занятиям
и самостоятельной работе
для студентов специальностей
080105 – Финансы и кредит
080502- Экономика и управление на предприятии (в машиностроении)
и направлений
080100 – Экономика
080500 – Менеджмент
Томск 2011
Общие положения. 3
1. Денежные потоки и методы их оценки. 4
1.1. Постоянный аннуитет. 4
1.2. Переменный аннуитет. 9
1.3. Бессрочный аннуитет. 15
1.4. Непрерывный аннуитет. 19
1.5. Метод депозитной книжки. 23
2. Управление оборотным капиталом предприятия. 27
3. Принятие управленческих решений на основе маржинального подхода. 32
4. Прогнозирование денежного потока. 38
Методические указания по выполнению самостоятельной работы.. 41
Общие положения
Методические указания практическим занятиям по дисциплине «Финансовый менеджмент» предназначены для студентов специальностей 080105- Финансы и кредит, 080502- Экономика и управление на предприятиях машиностроения и направлений 080500 - Менеджмент, 080100- Экономика.
Цель практических занятий– закрепить знания, полученные студентами на лекциях, научить проводить самостоятельные исследования по выбранной теме.
Каждое занятие содержит примеры решения типовых задач и предусматривает выполнение заданий. Выводы и заключения должны подтверждаться приведением цифровых данных из расчетной части работы.
Методические указания к практическим занятиям
Денежные потоки и методы их оценки
Постоянный аннуитет
Одним из ключевых понятий в финансовом менеджменте является понятие денежного потока как совокупности притоков и/или оттоков денежных средств, имеющих место через некоторые временные интервалы.
|
|
|
Оценка будущей стоимости постоянного аннуитета постнумерандо, платежи которого равны А, продолжительность аннуитета составляет n периодов и на каждый платеж один раз в конце каждого базового периода начисляются сложные проценты по ставке r, проводится по формуле:
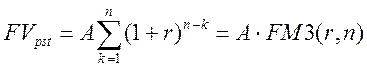(1.1)
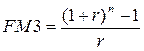
Оценка приведенной стоимости постоянного аннуитета постнумерандо, платежи которого равны А, продолжительность аннуитета составляет n периодов и на каждый платеж один раз в конце каждого базового периода начисляются сложные проценты по ставке r, проводится по формуле:
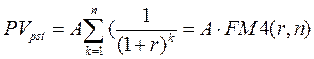(1.2)
Рассмотрим общую ситуацию, когда в течение базового периода денежные поступления происходят р раз и проценты начисляются m раз за период.
Формулы для оценки аннуитета постнумерандо
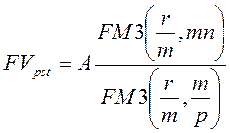(1.3)
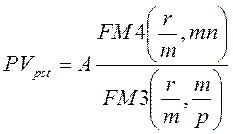(1.4)
Оценки постоянного аннуитета пренумерандо вычисляют по формулам:
(1. 5)
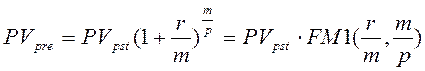(1.6)
Типовые задачи с решениями
Задача 1.
Предприниматель в результате инвестирования в некоторый проект будет получать в конце каждого квартала 8 тыс. долл. Определить возможные суммы, которые через три года получит предприниматель, если можно поместить деньги в банк под сложную процентную ставку 24% годовых с начислением процентов 1) ежегодно; 2)ежеквартально; 3)ежемесячно.
Решение
1) используем формулу (1.3) при А=8; n=3; r=24%; m=1; p=4:
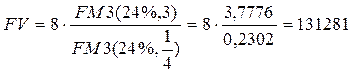, причем значение
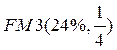вычисляем непосредственно по формуле
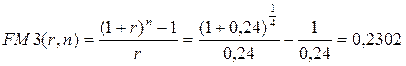
Через три года в банке на счете предпринимателя будет 131 281 000 долл.
2) Используем формулу (1.1), считая базовым периодом квартал, тогда А=8; n=12; r=6%:
FV=8×FM3(6%,12)=8×16,8699=134959
Через три года в банке на счете предпринимателя будет 134 959 000 долл.
3) используем формулу (1.3) при А=8; n=3; r=24%; m=1;,p=4:
FV=8×FM3 (2%,36)/FM3(2%,3)=8×51,9944/3,0606=135915
Через три года в банке на счете предпринимателя будет 135 915 000 долл.
Задача 2.
Какую сумму необходимо поместить в банк под сложную процентную ставку 6% годовых, чтобы в течение 6 лет иметь возможность в конце каждого года снимать со счета 100 тыс. руб., исчерпав счет полностью, если банком начисляются сложные проценты 1) ежегодно; 2) ежемесячно?
|
|
|
Решение
Для ответа на поставленный вопрос во всех случаях необходимо определить приведенную стоимость аннуитета постнумерандо.
1) по формуле (1.2) при А =100; r=6%; n=6:
PV=100×FM4(6%,6)=100×4,917=491,7
В банк на счет необходимо положить 491 700 руб.
2) по формуле (1.4) при А =100; r=6%; n=6; m=12:
PV=100×FM4(6/12;,72)/FM3(6/12;,12)=100∙4,8915=489,15
В банк на счет необходимо положить 489 150 руб.
Задача 3
Иванов должен Петрову 200 тыс. руб. Он предлагает вернуть долг равными ежегодными платежами в 50 тыс. руб. Через какое время долг будет погашен, если на него начисляются сложные проценты по ставке 12% годовых 1) ежемесячно; 2)ежеквартально; 3) ежегодно.
Решение
Выразим n из формулы (1.3), подставляя значения всех известных параметров.
1) формула (1.3) при А=50; r=0,12; m=12; p=1 имеет вид: 
из этой формулы находим n
n=5,92
Долг будет погашен через 5, 92 года
2) формула (1.3) при А=50; r=0,12; m=4 и p=1 имеет вид:
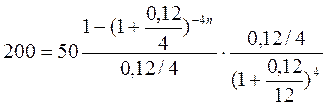
n=5,89
Долг будет погашен через 5, 89 года
3) формула (1.3) при А=50; r=0,12; m=1 и p=1 имеет вид
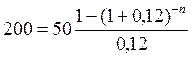
n=5,77
Долг будет погашен через 5,77 года
Задача 4
Господин Х выплатил жене при разводе 1 млн. руб. Жена после развода планирует получать ежемесячно одинаковые суммы в течение 20 лет. Какую сумму она будет получать, при условии, что процентная ставка по вкладам в банк равна 10% годовых?
Решение
1 млн. долл. – это приведенная стоимость срочной ренты постнумерандо, срок ренты- 20 лет, выплаты по ренте – ежемесячные. Величину неизвестного платежа находим из формулы (1.3) при PV =1 000 000; n=20; m=1, p=12:
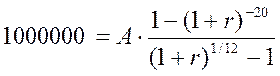
А=9336
Ежемесячно жена будет получать 9336 руб.
Задача 5
Фирме предложено инвестировать 200 млн. руб. на срок 4 года при условии возврата этой суммы частями (ежегодно по 50 млн. руб.); по истечении четырех лет будет выплачено дополнительное вознаграждение в размере 25 млн. руб. Примет ли она это предложение, если можно депонировать деньги в банк из расчета 8% годовых?
Решение
Определим сумму, которая накопится на счете, если положить деньги в банк:
|
|
|
F1=200 000 ∙(1+0,08)4= 272098
По формуле (1.1) при А=50000; r=8%; n=4 определим будущую стоимость аннуитета постнумерандо:
FV = 50000∙FM3(8%,4)=50000∙4,5061= 225305
С учетом дополнительного вознаграждения в 25 млн. руб., при условии инвестирования 200 млн., на конец четвертого года на счете фирмы будет сумма, равная
F2=225305+25000=250305
F1>F2, поэтому фирме более выгодно положить деньги в банк.
Задание к практическому занятию
Задача 1
Страховая компания заключила договор с предприятием на 5 лет, установив годовой страховой взнос в сумме 800 тыс. руб.. Страховые взносы помещаются в банк под сложную процентную ставку 10 % годовых, начисляемую ежемесячно. Определите сумму, которую получит по данному контракту страховая компания при следующих условиях: а) взносы поступают в конце года; б) взносы поступают равными долями в конце каждого полугодия (по 400 тыс. руб.); в).взносы поступают равными долями в конце каждого квартала (по 200 тыс. руб.).
Задача 2
Анализируются два плана накопления денежных средств по схеме аннуитета пренумерандо: 1) класть на депозит 200 тыс. руб. каждые полгода при условии, что банк начисляет сложные проценты по ставке 8%с ежеквартальным начислением процентов; 2) делать ежегодный вклад в размере 420 тыс. руб. при условии, что банк начисляет сложные проценты по ставке 7%с ежемесячным начислением процентов. Какая сумма будет на счете через 5 лет при реализации каждого плана?
Задача 3
Какую сумму необходимо поместить в банк под сложную процентную ставку 8% годовых, чтобы в течение 5 лет иметь возможность в конце каждого года снимать со счета 300 тыс. руб., исчерпав счет полностью, при следующих условиях: 1) банк начисляет сложные проценты ежеквартально; 2) банк начисляет сложные проценты ежемесячно?
Задача 4
Предприятие намеревается за 2 года создать фонд развития в сумме 5 млн. руб. Какую сумму предприятие должно ежемесячно ассигновать на эти цели при условии помещения этих денег в банк под сложную процентную ставку 8% годовых? Какой единовременный вклад в начале первого года нужно было бы сделать для создания фонда?
|
|
|
Задача 5
Какую сумму необходимо поместить в банк под процентную ставку 10% годовых, чтобы в течение 5 лет иметь возможность ежегодно получать по 120 тыс. руб., снимая деньги равными долями каждые 2 месяца (по 20 тыс. рублей) и в конце пятого года исчерпать счет полностью, если банком начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно?
Переменный аннуитет
Аннуитет называется переменным, если его члены различны по величине. Для оценки переменного аннуитета используют общие формулы оценки денежного потока. Если члены аннуитета изменяются в соответствии с некоторыми законами (в частности, образуют арифметическую или геометрическую прогрессию), то общие формулы для определения будущей или приведенной стоимости аннуитета можно упростить.
Пусть платежи аннуитета образуют арифметическую прогрессию, т.е. изменяются на постоянную абсолютную величину z и представляют собой последовательность:
A, A+z, A+2z, A+3z……A+(n-3)z, A+(n-2)z, A+(n-1)z.
Если z является положительной величиной, то платежи аннуитета возрастают. Если z является отрицательной величиной, то величина z и величина n (количество периодов аннуитета) связаны между собой соотношением:
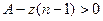откуда
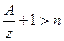
Формула для вычисления будущей стоимости аннуитета постнумерандо
(2.1)
Формула для вычисления приведенной стоимости аннуитета постнумерандо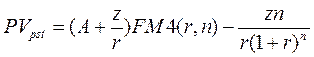 
(2.2)
Формулы для оценки будущей и приведенной стоимости аннуитета пренумерандо получаются из соотношений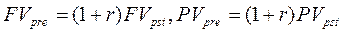 
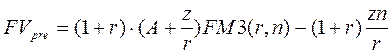(2.3)
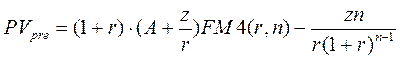(2.4)
Пусть платежи аннуитета образуют геометрическую прогрессию с первым членом А и знаменателем х. Т.е все платежи изменяются на одну и ту же относительную величину х и составляют ряд:
.
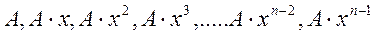Формулы для оценки переменного аннуитета постнумерандо, платежи которого образуют геометрическую прогрессию с первым членом А и знаменателем х:
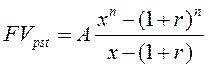(2.5)
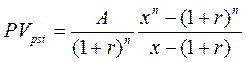(2.6)
Формулы для оценки переменного аннуитета пренумерандо, платежи которого образуют геометрическую прогрессию с первым членом А и знаменателем х:
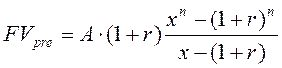(2.7)
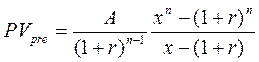(2.8)
|
|
|
