 |
Задание на практическую работу
|
|
|
|
Задача 1
В течение 5 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя в сумме 300 тыс. руб. Определите сумму, накопленную на счете к концу пятилетнего срока при использовании сложной процентной ставки 8% годовых, считая, что платежи поступают непрерывным образом.
Задача 2
Финансовая компания в соответствии со своими обязательствами должна выплачивать вкладчикам по 15 млн. руб. ежегодно в течение десяти лет. Какой суммой должна располагать компания, чтобы иметь возможность выполнить обязательства, если норма доходности составляет 10% за год и выплаты происходят постоянно и достаточно равномерно?
Задача 3
Месторождение полезных ископаемых будет разрабатываться в течение 8 лет, при этом ожидается, что доходы от эксплуатации месторождения составят в среднем 300 млн. руб. в год. Определите приведенную стоимость ожидаемого дохода при использовании сложной процентной ставки 10% годовых и в предположении, что отгрузка и реализация продукции будут непрерывны и равномерны.
Задача 4
Финансовая компания в течение трех лет в соответствии со своими обязательствами должна выплачивать вкладчикам 8 млн. руб. ежегодно. Какой суммой должна располагать компания, чтобы иметь возможность выполнить обязательства, если норма доходности составляет 12 % за год и выплаты происходят постоянно и достаточно непрерывно?
Задача 5
Фирма намеревается выпускать некоторую продукцию в течение 4 лет, получая ежегодно выручку в размере 50 млн. руб. Предполагается, что продукция в течение года будет продаваться равномерно. Оцените ожидаемый доход фирмы, если применяется непрерывная ставка 22% за год.
|
|
|
Метод депозитной книжки
Рассмотрим методы погашения ссуды, выданной под сложный ссудный процент, начисляемый на непогашенный остаток ссуды. Ссуда погашается равными годовыми платежами, поэтому при вычислении платежей можно использовать формулы для аннуитетов. Погашение исходного долга осуществляется постепенно в течение всего срока действия аннуитета. Структура годового платежа постоянно меняется — в начальные периоды в нем преобладают начисленные за очередной период проценты; с течением времени доля процентных платежей постоянно уменьшается и повышается доля погашаемой части основного долга.
Типовые задачи с решениями
Задача 1
В банке получена ссуда на пять лет в сумме 20 000 долл. под 13 % годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Требуется определить величину годового платежа.
Решение.
Если обозначить за A величину искомого годового платежа, то данный финансовый контракт можно представить в виде следующей схемы (5.1).
 |
Для лучшего понимания логики метода депозитной книжки целесообразно рассуждать с позиции кредитора. Для банка данный контракт представляет собой инвестицию в размере 20 000 долл., т.е. отток денежных средств, что и показано на схеме. В дальнейшем в течение пяти лет банк будет ежегодно получать в конце года сумму А, причем каждый годовой платеж будет включать проценты за истекший год и часть основной суммы долга. Так, поскольку в течение первого года заемщик пользовался ссудой в размере 20 000 долл., то платеж, который будет сделан в конце этого года, состоит из двух частей: процентов за год в сумме 2600 долл. (13 % от 20 000 долл.) и погашаемой части долга в сумме (А - 2600) долл. В следующем году расчет будет повторен при условии, что размер кредита, которым пользуется заемщик, составит уже меньшую сумму по сравнению с первым годом, A именно
|
|
|
(20 000 – A + 2600) долл. Отсюда видно, что с течением времени сумма уплачиваемых процентов снижается, A доля платежа в счет погашения долга возрастает. Из схемы на рис. 4.9 видно, что мы имеем дело с аннуитетом постнумерандо, о котором известны его текущая стоимость, процентная ставка и продолжительность действия. Поэтому для нахождения величины годового платежа A можно воспользоваться формулой (4.16):
20000 = FM 4(13 %,5)∙ А = 3,517∙А, т.е. A = 5687 долл.
Динамика платежей показана в табл. 4.1. Отметим, что данные в ходе вычислений округлялись, поэтому величина процентов в последней строке найдена балансовым методом.
Таблица 5.1.Метод депозитной книжки
| Год | Остаток ссуды на начало года | Сумма годового платежа | В том числе | Остаток ссуды на конец года | |
| проценты за год | погашенная часть долга | ||||
Данная таблица позволяет ответить на целый ряд дополнительных вопросов, представляющих определенный интерес для прогнозирования денежных потоков. В частности, можно рассчитать общую сумму процентных платежей, величину процентного платежа в k -м периоде, долю кредита, погашенную в первые k лет, и т.д.
Рассуждения, аналогичные используемым при решении примера, можно провести и в общем виде, что позволит дать более строго интерпретацию приведенной стоимости аннуитета с помощью метода депозитной книжки и попутно выявить полезные с финансовой точки зрения закономерности, позволяющие ответить на многие вопросы, связанные с денежными потоками.
Итак, пусть получена ссуда в сумме S на n лет под процентную ставку r, причем сложные проценты начисляются на непогашенный остаток. Определим величину годового платежа при возврате долга равными суммами в конце каждого года.
Обозначим через A годовой платеж. В конце первого года часть его, равная Sr, идет на уплату процентов. Оставшаяся же часть A - Sr — на уплату части долга. Таким образом, к концу первого года величина непогашенного остатка составит: S - (A - Sr)= S (1 + r) - A.
В конце второго года на уплату процентов пойдет уже величина (S (1 + r) - A) r, A на уплату долга — A - (S (1 + г) - А) r = =(A - Sr)(1 + r). Следовательно, к концу второго года долг будет равен:
|
|
|

В конце третьего года проценты и уплата долга соответственно составят:

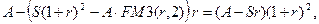
следовательно, остаток долга станет равным:

Вообще можно доказать, что в конце k -го года (k =1, 2,..., n) проценты, уплата долга и непогашенный остаток соответственно составят:
 (5.1)
(5.1)
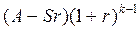 (5.2)
(5.2)
 (5.3)
(5.3)
Поскольку долг должен быть выплачен через n лет, то справедливо равенство S (1 + r) n – A∙FM 3(r,n) = 0, откуда

Следовательно, S является приведенной стоимостью постоянного аннуитета постнумерандо с членом, равным А, т.е.

Используя формулы (5.1) — (5.3), можно различным образом характеризовать денежные потоки. Например, найти сумму процентных платежей за m лет (m = 1, 2,..., n):
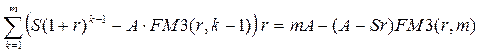
откуда, в частности, следует, что доля кредита, погашенная в первые m лет, составит (A - Sr) FM 3(r, m).
Проверим некоторые вычисления приведенного примера. Поскольку для него  = 20 000, n = 5, A = 5687, то из (5.1) можно найти величину процентного платежа в четвертом периоде:
= 20 000, n = 5, A = 5687, то из (5.1) можно найти величину процентного платежа в четвертом периоде:
(20000∙(1 + 0,13)3 – 5687∙ FM 3(13 %,3))∙0,13 = 1233,
что совпадает с соответствующим значением в табл. 5.1.
|
|
|


