 |
Задание к практическому занятию
|
|
|
|
Задача 1
Определить ежемесячные поступления бессрочного аннуитета постнумерандо, если его приведенная стоимость равна 100 тыс. руб. и предлагаемый государственным банком процент по срочным вкладам равен 12 % годовых, начисляемых ежеквартально.
Задача 2
Фирма собирается учредить фонд для ежегодной выплаты пособий своим работникам. Выплаты будут производиться в конце года. Определить сумму, которую фирма должна поместить на депозит в банк, чтобы обеспечить получение неограниченно долго в конце каждого года 1 млн. руб., если банк начисляет: а) ежегодно сложные проценты по ставке 10 %; б) ежеквартально сложные проценты по ставке 10 %; в) непрерывные проценты с силой роста 10 %.
Задача 3
Определить текущую (приведенную) стоимость бессрочного аннуитета постнумерандо с ежемесячными поступлениями в сумме 10 тыс. руб., если предлагаемый государственным банком процент по срочным вкладам равен 14 % годовых, начисляемых ежеквартально.
Задача 4
Компания за предыдущий год выплатила 1 тыс. руб. за акцию. Согласно прогнозам, дивиденды по акциям этой компании будут расти на 50 руб. ежегодно в течение неопределенно долгого времени. Сделайте вывод о целесообразности покупки акций компании по цене 21 тыс. руб., если можно поместить деньги в банк на депозит под 10% годовых.
Задача 5
Стоит ли покупать за 55 000 руб. ценную бумагу, генерирующую ежегодный доход в сумме 60 000 руб. в течение 50 лет? При расчетах использовать сложную ставку 10% годовых, начисляемую ежеквартально.
Непрерывный аннуитет
Если в течение каждого базового периода денежные поступления происходят очень часто, так что промежутки между последовательными поступлениями представляют собой бесконечно малые величины, то аннуитет считают непрерывным.
|
|
|
Оценки будущей и приведенной стоимости непрерывного аннуитета, на платежи которого начисляются дискретные проценты:
(4.1)
Приведенная стоимость этого непрерывного аннуитета составит:
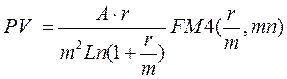(4.2)
Таким образом, переход от дискретных платежей постнумерандо к непрерывным, приводит к увеличению приведенной и будущей стоимости аннуитета в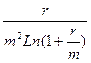 
раз.
Оценки непрерывного аннуитета в случае начисления непрерывных процентов:
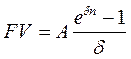(4.3)
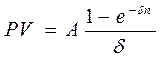(4.4)
Типовые задачи с решениями
Задача 1
В течение 4 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя в сумме 10 млн. руб. Определите сумму, накопленную к концу четвертого года при использовании процентной ставки 15% годовых, если начисление сложных процентов осуществляется ежегодно.
Решение
Поскольку платежи поступают достаточно часто, можно считать, что они поступают непрерывным образом. Тогда можно воспользоваться формулой (4.1) для определения наращенной суммы непрерывного аннуитета при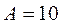 
; n =4, т =1, r =0,15:
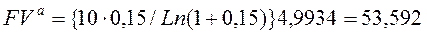
К концу четвертого года на счете в банке накопится 53 592 000 руб.
Сравним этот результат со значением, полученным по формуле р- срочного аннуитета постнумепрандо при р = 360; А = 10/360; n =4, т =1, r =0,15:
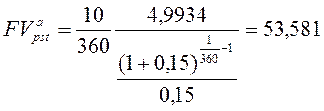
К концу четвертого года на счете в банке накопится 53 581 000 руб.
Полученные величины отличаются на 3000 руб..
Задача 2
Фирма намеревается выпускать некоторую продукцию в течение трех лет, получая ежегодно выручку в размере 300 млн. руб. Предполагается, что продукция в течение года будет продаваться равномерно. Оцените ожидаемые денежные поступления, если применяется непрерывная ставка 20% годовых.
Решение
Поскольку в условии говорится о равномерном распределении продаж в течение года, то что интенсивность потока выручки будет постоянной величиной, равной 300 млн. руб. в год. Считая, что денежные поступления происходят непрерывно, воспользуемся формулами для определения соответственно будущей и приведенной стоимости непрерывного аннуитета (4.3) и (4.4). Полагая 
; п = 3; s = 0,2, получим:
|
|
|
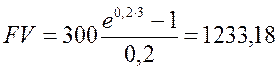
Оценка денежных поступлений на момент окончания третьего года равна 1233, 18 млн. руб.
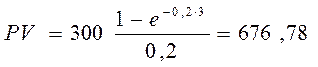
Дисконтированная оценка денежных поступлений на момент начала первого года равна 676,78 млн. руб.
Задача 3
Финансовая компания в соответствии со своими обязательствами должна выплачивать вкладчикам по 20 млн. руб. ежегодно в течение пяти лет. Какой суммой должна располагать компания, чтобы иметь возможность выполнить обязательства, если норма доходности составляет 10% за год и выплаты происходят постоянно и достаточно равномерно?
Решение
Для решения задачи необходимо найти приведенную стоимость непрерывного аннуитета по формуле (4.2) при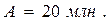 
; n=5; m=1; r =0,10:
млн.
Таким образом, имея 79,54 млн. руб. компания способна выполнить свои обязательства перед вкладчиками.
Для определения срока аннуитета при прочих известных параметрах используют формулы:
Задача 4
За какой срок наращенная сумма ренты вырастет в 5 раз по сравнению с годовой суммой взносов, если взносы поступают непрерывно и равномерно в течение года и на взносы начисляются проценты с силой роста 8%?
Решение
По условию задачи известно, что наращенная сумма непрерывного аннуитета с непрерывным начислением процентов в 5 раз больше годового платежа аннуитета. Неизвестный срок такого аннуитета можно выразить из формулы (4.3):
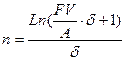
Подставим в полученное выражение значения 
, получим:
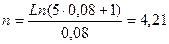
Наращенная сумма ренты возрастет в 5 раз по сравнению с годовой суммой взносов за 4, 21 года.
Задача 5
Десятилетняя рента с ежегодными суммарными платежами в размере 1 млн. руб. выкупается за 4 млн.руб. Определить срок этой ренты, если на платежи начисляются непрерывные проценты по ставке 10% годовых.
Решение
По условию задачи известна приведенная стоимость непрерывной ренты с непрерывным начислением процентов. Срок ренты можно выразить из формулы (4.4):
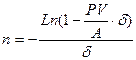
Подставим в полученное выражение значения А=1; n=10; PV=4;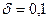 
, получим
|
|
|
=5,11
Срок ренты равен 5,11 года.
|
|
|
