Определители. Свойства определителей. Примеры.

Матрицы. Основные понятия.

Матрицей называется прямоугольная таблица чисел, содержа­щая т строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде

или сокращенно, А=(а_ij), где i= l, m(т.е. i=1,2,3,…,m)- номер строки, i= l,n(т.е. i= 1,2,3,…,n) –номер столбца. Матрицу А называют матрицей размера m_*n и пишут Аm_*n _*Числа a_ij, составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из левого верхнего угла, образуют главную диагональ матрицы. Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е. А= В, если a_ij = b_ij, где i = l,m, j = l,n.

Классификация матриц: квадратная, диагональная и т.д.

Транспонирование матрицы. Примеры.

Матрица, у которой число строк равно числу столбцов, назы­вается квадратной. Квадратную матрицу размера п х п называют матрицей n-го порядка. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е. Так, единичная матрица 3-го порядка имеет вид

Квадратная матрица называется треугольной, если все элемен­ты, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нуле­вой. Обозначается буквой О. Имеет вид

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике. Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка, соответственно). Их вид:

Матрица, полученная из данной заменой каждой ее строки столб­цом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^т. Так если А^т =(1 0)

Матрицы. Действия над матрицами Примеры.

Операция сложения матриц вводится только для матриц одина­ковых размеров. Например,

+ =

Аналогично определяется разность матриц.

Произведением матрицы А_т*п — (а_ij) на число k

Матрица -A = (-1) * А называется противоположной матри­це А.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

 

4. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду. Примеры.

Элементарными преобразованиями матрицы называются следующие ее преобразования: I. Перестановка двух столбцов (строк) матрицы. II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля. III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.

Невырожденные матрицы. Обратная матрица. Примеры.

Матрица А^-1 наз. обратной для матрицы А, если А^-1 А = Е Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. А 0. Элемент обратной матрицы (А^-1)_{i j} равен алгебраическому дополнению A_{j i} матрицы А, деленному на det A: (A^-1)_{i j} = A_{j i} / det A (индексы поменяли места) или A^-1 = (detA)^-1 ||A_ij||^T Пример: Построить матрицу обратную к данной. 3 -1 -1 det ^ A =52

А= 2 2 4 A ₁₁=14 A ₁₂ =-6 A ₁₃ =-4 A ₂₁ =4 A ₂₂ =2 A ₂₃ =10

-1 -3 1 A ₃₁ =-2 A ₃₂ =-14 A ₃₃ =8

Составим из них присоединённую матрицу и транспонируем ее и вычислим по формуле A ^–1 = (det A)^–1|| A_ij || ^T . И после вычислим произведение. Получилась единичная матрица.

Алгоритм нахождения обратной матрицы Примеры.

1. Вычисление определителя матрицы A. Если он не равен нулю, продолжаем решение, иначе - обратной матрицы не существует.

2. Нахождение транспонированной матрицы A^T.

3. Определение алгебраических дополнений.

4. Составление обратной матрицы из алгебраических дополнений.

Определители 2-го и 3-го порядка. Основные понятия. Примеры.

Определение и основные свойства (транспонирование, изменение порядка строк или столбцов, умножение на число, сложение строк или столбцов, разложение определителя по элементам строки или столбца).

Определители. Свойства определителей. Примеры.

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть

.

СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,

.

СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,

.

СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

.

Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.

СВОЙСТВО 9. Определитель

равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

, ,

, ,

, .

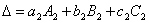12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: