Общее уравнение плоскости.

Приведем формулировку теоремы, которая дает нам вид уравнения плоскости.

Теорема.

Всякое уравнение вида , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида .

Уравнение называется общим уравнением плоскости в пространстве. Если не придавать числам А, В, С и D конкретных значений, то общее уравнение плоскости называют уравнением плоскости в общем виде.

Следует заметить, что уравнение вида , где - некоторое действительное число, отличное от нуля, будет определять ту же самую плоскость, так как равенства и эквивалентны. К примеру, общие уравнения плоскости и задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.

Немного поясним смысл озвученной теоремы. В прямоугольной системе координат Oxyz каждой плоскости соответствует ее уравнение общего вида , а каждому уравнению соответствует плоскость в заданной прямоугольной системе координат трехмерного пространства. Другими словами, плоскость и ее общее уравнение неразделимы.

Если все коэффициенты А, В, С и D в общем уравнении плоскости отличны от нуля, то оно называется полным. В противном случае, общее уравнение плоскости называется неполным.

Неполными уравнениями задаются плоскости, параллельные координатным осям, проходящие через координатные оси, параллельные координатным плоскостям, перпендикулярные координатным плоскостям, совпадающие с координатными плоскостями, а также плоскости, проходящие через начало координат.

Например, плоскость параллельна оси абсцисс и перпендикулярна координатной плоскости Oyz, уравнение z = 0 определяет координатную плоскость Oxy, а общее уравнение плоскости вида соответствует плоскости, проходящей через начало координат.

Отметим также, что коэффициенты A, B и C в общем уравнении плоскости представляют собойкоординаты нормального вектора плоскости.

Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.

Рекомендуем ознакомиться с материалом статьи общее уравнение плоскости, где информация по теме изложена детальнее, подробно разобраны решения характерных примеров и задач.

Проходящей через три точкки.. Прежде чем приступать к составлению уравнения плоскости, проходящей через три заданные точки пространства, вспомним одну аксиому: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость. Таким образом, задав три различных и не лежащих на одной прямой точки, мы в трехмерном пространстве однозначно определим плоскость, проходящую через эти точки.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, в ней заданы три несовпадающие точки , которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.

Покажем два способа ее решения.

Первый способ составления уравнения плоскости, проходящей через три заданные точки .

Известно, что общее уравнение плоскости вида задает в прямоугольной системе координат Oxyz плоскость , которая проходит через точку , а нормальный вектор плоскости имеет координаты . Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки .

Итак, из условия задачи нам известны координаты точки (даже координаты трех точек), через которую проходит плоскость, уравнение которой нам требуется составить. Осталось отыскать координаты нормального вектора 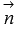этой плоскости.

Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости перпендикулярны, то вектор 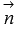перпендикулярен как вектору , так и вектору . Следовательно, в качестве вектора 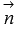можно принять векторное произведение векторов и . Так как и (при необходимости обращайтесь к статье вычисление координат вектора по координатам точек), то . После вычисления записанного определителя, станут видны координаты нормального вектора 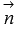, и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.