 |
Основные теоремы о пределах (сумма пределов, произведение пределов, предел дроби и т.д.). Первый и второй замечательные пределы.
|
|
|
|
Эквивалентные бесконечно малые функции. Применение при вычислении пределов.
Непрерывность функций. Точки разрыва и их классификация.
Основные элементарные функции и их графики.
Основные теоремы о непрерывных функциях. Свойства функций, непрерывных на отрезке.
Производная функции. Определение производной; ее геометрический и механический смысл.
Производная суммы, разности, произведения и р
Производные основных элементарных функций. Таблица производных.
Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование.
Производные высший порядков (заданных явно, параметрически, неявно).
Дифференциал функции. Таблица дифференциалов.
Исследование функций при помощи производных (возрастание и убывание функции, точки экстремума, выпуклость функции, асимптоты).
57.Правила Лопиталя (раскрытие неопределенности( ).
).
Общая схема исследования функции и построения графика.
Комплексные числа. Основные понятия. Геометрическое изображение и форма записи комплексного числа.
Комплексные числа. Действия над комплексными числами.
Неопределенный интеграл. Понятие и свойства неопределённого интеграла.
Таблица основных неопределенных интегралов.
Основные методы интегрирования (метод непосредственного интегрирования, метод интегрирования подстановкой)
Основные методы интегрирования. Метод интегрирования по частям.
Интегрирование рациональных дробей. Интегрирования простейших рациональных дробей.
Интегрирование тригонометрических функций (универсальна подстановка, использование тригонометрических преобразований).
|
|
|
Интегрирование иррациональных функций (дробно –линейная подстановка, тригонометрическая подстановка)
68. Интегрирование дифференциального бинома  .
.
Определённый интеграл. Формула Ньютона – Лейбница.
Основные свойства определенного интеграла.
Вычисление определенного интеграла. Формула Ньютона – Лейбница. Интегрирование подстановкой. Интегрирование по частям.
Даны вершины треугольника. Найти внутренний угол при вершине В.
Найти площадь треугольника с вершинами.
74. Найти объём треугольной пирамиды, построенной на векторах 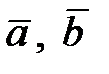 и
и  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.
Решить систему линейных уравнений матричным способом.
78. Найти площадь параллелограмма, построенного на векторах  и
и  (с помощью элементов векторной алгебры).
(с помощью элементов векторной алгебры).
79. Найти объём параллелепипеда, построенной на трех векторах 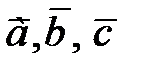 .
.
Вычислить определитель различными способами.
Найти матрицу обратную данной
82.Найти угол между векторами  .
.
83. Доказать, что четыре точки О, А, В, С лежат в одной плоскости.
84. Найти произведение матриц А и В (если это возможно).
Привести матрицу к ступенчатому виду.
Найти ранг матрицы.
87. Составить уравнение сторон треугольника АВС.
Уравнение прямой привести к различным видам(уравнение прямой с угловым коэффициентом, уравнение прямой в отрезках, нормальное уравнение прямой).
Найти точку пересечения прямых и угол между ними.
Определить вид линии и построить её.
Найти производные данных функций.
Найти пределы.
Исследовать данную функцию и построить график.
Найти пределы правилом Лопиталя.
Найти дифференциал.
Вычислить интеграл.
Найти наибольшее и наименьшее значение функции на отрезке.
|
|
|
Найти экстремумы функции.
Определить промежутки возрастания и убывания функции.
|
|
|


