 |
Системы линейных уравнений. Формулы Крамера решения систем линейных уравнений. Пример.
|
|
|
|
Еще одним популярным методом решения системы линейных алгебраических уравнений является метод Крамера. Крамера, используя следующие формулы: для вычисления корней уравнений xi (i=1,n)
xi=Δin/Δn (i=1,n),
где Δn=det A, а Δin являются определителями n-го порядка, которые получаются из Δn путем замены в нем i-го столбца столбцом свободных членов исходной системы.
Что бы закрепить теоретический материал, обратимся к практике, решим систему из трех уравнений методом Крамера.
76x1-7x2-6x3=-5
10x1+12x2-7x3=11
-16x1+10.5x2-13x3=-10
Определим совместность системы линейных уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что бы ранг основной матрицы
| A= |
|
и ранг расширенной матрицы
| B= |
|
были равны.
Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.
Согласно вышеприведенной формуле для метода Крамера, необходимо найти главный определитель и он будет равен
| Δ= |
| =-9746 |
Для вычисления X1 найдем первый определитель, для чего заменим первый столбец столбцом свободных членов.
| Δ1= |
| =-2491.5 |
Точно как же как и для X1 найдем определитель, для вычисления X2
| Δ2= |
| =-17854 |
Проделаем аналогичную операцию для вычисления следующего определителя для X3
| Δ3= |
| =-18851 |
В результате осталось разделить нужные определители на главный, в итоге получим:
X1=Δ1/Δ?0.256
X2=Δ2/Δ?1.832
X3=Δ3/Δ?1.934
|
|
|
Системы линейных однородных уравнений, условия совместности и методы решения.
Векторы. Основные понятия.
Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны.Единичным вектором или ортом - называется вектор, длина которого равна единице.
Векторы. Линейные операции над векторами. Примеры.
Сложение векторов. Пусть 
и 
– два произвольных вектора. Возьмем произвольную точку О и построим вектор 
; затем от точки А отложим вектор 
. Вектор 
, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается 
Вычитание векторов. Разностью 
векторов и называется такой вектор 
, который в сумме с вектором дает вектор : 
Û 
. Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» 
Умножение вектора на число. Произведением вектора на действительное число 
называется вектор (обозначают 
), определяемый следующими условиями:
|
|
|
1) 
,
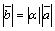2) 
при 
и 
при 
.
Очевидно, что при 
.
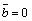Построим, например, векторы 
и 
для заданного вектора
|
|
|
