 |
Смешанное произведение векторов. Свойства смешанного произведения. Геометрический смысл.
|
|
|
|
Выясним геометрический смысл смешанного произведения векторов 
и 
.
Отложим векторы и от одной точки и построим параллелепипед на этих векторах как на сторонах.
Обозначим 
. В этом случае смешанное произведение можно записать как 
, где 
- числовая проекция вектора на направление вектора .
Абсолютная величина числовой проекции равна высоте параллелепипеда, построенного на векторах и , так как вектор перпендикулярен и вектору 
и вектору 
по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина 
представляет собой площадь параллелограмма, построенного на векторах и . Таким образом, модуль смешанного произведения 
- это произведение площади основания на высоту параллелепипеда, построенного на векторах и .
Следовательно, абсолютная величина смешанного произведения векторов представляет собой объем параллелепипеда: 
. В этом заключается геометрический смысл смешанного произведения векторов.
Объем тетраэдра, построенного на векторах и , равен одной шестой объема соответствующего параллелепипеда, таким образом, 
.
Система координат на плоскости. Связь между прямоугольными и полярными координатами.
Пусть M – произвольная точка плоскости, x, y –её прямоугольные координаты, а
ρ,φ – полярные координаты (рисунок ниже).
Тогда
Пример 1
Прямоугольные координаты точки равны x=4, y=-4. Найти её полярные координаты.
Решение.
Значит
так как точка лежит в четвёртой четверти, то первое значение правильно.
Главное значение φ есть -π/4.
Пример 2
Определить какую линию представляет уравнение
Решение.
Переходя к прямоугольной системе, находим
|
|
|
Простейшие задачи аналитической геометрии на плоскости.
Простейшие задачи аналитической геометрии
Расстояние между двумя точками
где 
и 
радиус-векторы точек 
и 
.
В координатах:
на прямой 
на плоскости 
в пространстве 
Деление отрезка в данном отношении 
В координатах:
на прямой 
;
на плоскости , 
;
в пространстве , , 
Линия на плоскости. Основные понятия.
Определение. Линия на плоскости – множество точек плоскости, обладающих некоторым только им присущим геометрическим свойством.
Определение. Уравнением линии на плоскости 
называется такое уравнение 
с двумя переменными, которому удовлетворяют координаты каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Определение. Уравнением линии в полярной системе координат называется уравнение 
, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
Линию на плоскости можно задать параметрическими уравнениями 
где 
и 
– непрерывны по параметру 
. Чтобы перейти от параметрических уравнений к уравнению вида надо из двух уравнений исключить параметр .
Пример. Какая линия определяется параметрическими уравнениями 
?
Решение. Исключая параметр , приходим к уравнению 
. В силу параметрических уравнений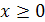 
, 
. Следовательно, данные параметрические уравнения определяют луч – биссектрису I-го координатного угла.
Линию на плоскости можно задать векторным уравнением 
, где – скалярный переменный параметр. Этому уравнению в системе координат соответствуют два скалярных уравнения 
.
Векторное уравнение и параметрические уравнения линии имеют механический смысл: при перемещении точки на плоскости указанные уравнения называются уравнениями движения, а линия – траекторией точки, параметр при этом есть время.
|
|
|
