 |
Бесконечно большая функция. Бесконечно малые функции. Определения и основные теоремы.
|
|
|
|
Расстановка ударений: БЕСКОНЕ`ЧНО БОЛЬША`Я ФУ`НКЦИЯ
БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:
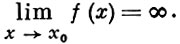
Аналогичным образом определяются

Напр.,
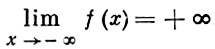
означает, что для любого М > 0 найдется такое δ = δ (M) > 0, что для всех z < - δ выполняется неравенство f(x) > M. Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функций, т. к. если f(x) есть Б. б. ф., то функция ψ (х) = 1/f(x) является бесконечно малой.
Функция α (x) называется бесконечно малой при  , если
, если
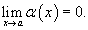
Предположим, что α (x) и β (x) - бесконечно малые функции при  .
.
· Если 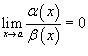 , то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);
, то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);
· Если  , то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;
, то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;
· Если  , то говорят, что функция α (x) является бесконечно малой порядка n относительно функции β (x);
, то говорят, что функция α (x) является бесконечно малой порядка n относительно функции β (x);
· Если  , то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при
, то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при  .
.
· Теорема. Если  — бесконечно большая последовательность и все ее элементы отличны от нуля (
— бесконечно большая последовательность и все ее элементы отличны от нуля ( ), то последовательность
), то последовательность  — бесконечно малая, и наоборот, если
— бесконечно малая, и наоборот, если 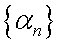 — бесконечно малая последовательность и все ее элементы отличны от нуля (
— бесконечно малая последовательность и все ее элементы отличны от нуля ( ), то последовательность
), то последовательность  =
=  — бесконечно большая. Доказательство. Докажем первое утверждение теоремы. Пусть
— бесконечно большая. Доказательство. Докажем первое утверждение теоремы. Пусть  — бесконечно большая последовательность, т.е. для любого
— бесконечно большая последовательность, т.е. для любого  найдется номер элемента последовательности
найдется номер элемента последовательности  такой, что для всех
такой, что для всех  выполняется соотношение
выполняется соотношение  . Требуется доказать, что последовательность
. Требуется доказать, что последовательность  — бесконечно малая.Зададим произвольное
— бесконечно малая.Зададим произвольное  . Покажем, что существует
. Покажем, что существует  такое, что для всех
такое, что для всех  выполняется соотношение
выполняется соотношение  . Возьмем
. Возьмем  . По определению бесконечно большой последовательности, начиная с
. По определению бесконечно большой последовательности, начиная с  все элементы последовательности удовлетворяют соотношению
все элементы последовательности удовлетворяют соотношению  . Следовательно, начиная с
. Следовательно, начиная с  выполняется
выполняется  или
или  . Аналогично доказывается второе утверждение теоремы. Теорема. Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности. Доказательство. Пусть
. Аналогично доказывается второе утверждение теоремы. Теорема. Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности. Доказательство. Пусть 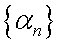 и
и  — две бесконечно малые последовательности. Покажем, что последовательности
— две бесконечно малые последовательности. Покажем, что последовательности 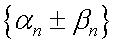 также бесконечно малые. Зададим произвольное
также бесконечно малые. Зададим произвольное  . По определению бесконечно малых последовательностей существуют
. По определению бесконечно малых последовательностей существуют  и
и  такие, что для всех
такие, что для всех  :
:  и для всех
и для всех  :
:  . Возьмем
. Возьмем  , тогда для всех
, тогда для всех  :
:  . Что и требовалось доказать. Следствие. Сумма или разность любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Теорема. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность. Доказательство. Пусть
. Что и требовалось доказать. Следствие. Сумма или разность любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Теорема. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность. Доказательство. Пусть  и
и  — две бесконечно малые последовательности. Покажем, что
— две бесконечно малые последовательности. Покажем, что  также бесконечно малая. Зададим произвольное
также бесконечно малая. Зададим произвольное  . Так как
. Так как  — бесконечно малая, то существует
— бесконечно малая, то существует  такое, что для всех
такое, что для всех  :
:  . Так как
. Так как  — бесконечно малая, то существует
— бесконечно малая, то существует  такое, что для всех
такое, что для всех  :
:  . Возьмем
. Возьмем  , тогда для всех
, тогда для всех  :
:  . Что и требовалось доказать. Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Замечание. Теорема о сумме и разности не имеет аналога для бесконечно больших последовательностей. Действительно, сумма двух бесконечно больших последовательностей в общем случае может быть какой угодно. Например,
. Что и требовалось доказать. Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Замечание. Теорема о сумме и разности не имеет аналога для бесконечно больших последовательностей. Действительно, сумма двух бесконечно больших последовательностей в общем случае может быть какой угодно. Например,  — ограниченная последовательность
— ограниченная последовательность  ;
;  — бесконечно большая последовательность
— бесконечно большая последовательность  ;
;  — бесконечно малая последовательность
— бесконечно малая последовательность  . Замечание. Теорема о произведении обобщается на случай бесконечно больших последовательностей. Замечание. Частное двух бесконечно малых (больших) последовательностей может быть последовательностью, сходящейся к любому числу, а может и не сходиться вовсе. Например, если
. Замечание. Теорема о произведении обобщается на случай бесконечно больших последовательностей. Замечание. Частное двух бесконечно малых (больших) последовательностей может быть последовательностью, сходящейся к любому числу, а может и не сходиться вовсе. Например, если  ,
,  , то
, то  — бесконечно большая последовательность;
— бесконечно большая последовательность;  — бесконечно малая последовательность. Теорема. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность. Доказательство. Пусть
— бесконечно малая последовательность. Теорема. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность. Доказательство. Пусть  — ограниченная последовательность, а
— ограниченная последовательность, а  — бесконечно малая. Покажем, что
— бесконечно малая. Покажем, что  — бесконечно малая. Зададим произвольное
— бесконечно малая. Зададим произвольное  . Так как
. Так как  — ограниченная последовательность, то существует
— ограниченная последовательность, то существует  такое, что
такое, что  . Так как
. Так как  — бесконечно малая, то существует
— бесконечно малая, то существует  такое, что для всех
такое, что для всех  :
:  . Тогда для всех
. Тогда для всех  :
: 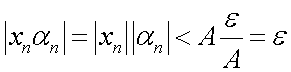 . Что и требовалось доказать. Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
. Что и требовалось доказать. Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
|
|
|
|
|
|
|
|
|


