 |
Основные свойства функции.
|
|
|
|
1. Четность и нечетность
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
График нечетной функции симметричен относительно начала координат.
Монотонность (возрастание, убывание)
Пример:
Функция f(x) возрастает на множестве Р, если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
Функция f(x) убывает на множестве Р, если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
42.Последовательности. Числовая последовательность. Предел числовой последовательности. Число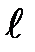 
.Натуральный логарифм.
Числовая последовательности и ее предел.
Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае
Числовой последовательностью называется бесконечное множество чисел
(1)
следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого 
задается как функция целочисленного аргумента, 
т.е. 
.
Число А называется пределом последовательности (1), если для любого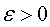 
существует число 
, такое, что при 
выполняется неравенство 
. Если число А есть предел последовательности (1), то пишут
Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.
|
|
|
Для сходящихся последовательностей имеют место теоремы:
если 
.
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
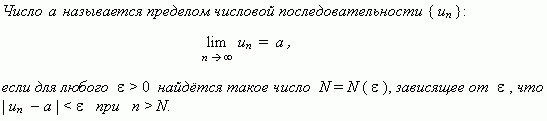
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a -, a +). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что | un | 
M для всех n. Возрастающая или убывающая последовательность называется монотонной.
43.Предел функции. Предел функции в точке. Односторонние пределы. Предел функции при 
.
Односторонние пределы
В определении предела функции 
считается, что х стремится к x0 любым способом: оставаясь меньшим, чем x0 (слева от х0), большим, чем хо (справа от хо), или колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента х к хо существенно влияет на значение придела функции. Поэтому вводят понятия односторонних пределов.
Число А1 называется пределом функции у=ƒ(х) слева в точке хо, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х0-δ;xo), выполняется неравенство |ƒ(х)-А|<ε. Предел слева записывают так: limƒ(х)=А при х–>х0-0 или коротко: ƒ(хо-0)=А1 (обозначение Дирихле) (см. рис. 111).
Аналогично определяется предел функции справа, запишем его с помощью символов:
|
|
|
Коротко предел справа обозначают ƒ(хо+0)=А.
Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует , то существуют и оба односторонних предела, причем А=А1=А2.
Справедливо и обратное утверждение: если существуют оба предела ƒ(х0-0) и ƒ(х0+0) и они равны, то существует предел и А=ƒ(х0-0).
Если же А1¹А2, то етот придел не существует.
Предел функции при х ® ∞
Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→ ∞, если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|<ε. Коротко это определение можно записать так:
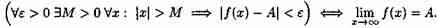
Геометрический смысл этого определения таков: для "ε>0 $ М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).
|
|
|
