 |
Математическая модель балансовых задач
|
|
|
|
Раздел 1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ВАРИАНТЫ ЕЕ ОСНОВЫ
Основные понятия и определения
Определение1. Модель – это образ или отражение какого - либо процесса или явления, полученное с помощью специальных средств. Специальными средствами могут быть: математические, технические, физические, компьютерные, имитационные и т. д. Поясняя в определении 1 специальные средства, будем иметь соответствующие модели.
Определение 2. Математическая модель - это образ или отражение какого - либо процесса или явления, полученное с помощью математических средств.
Определение 3. Компьютерная модель – это образ или отражение какого – либо процесса или явления, полученное с помощью компьютерных средств.
Определение 4. Процесс получения моделей называют моделированием.
Следует отметить, что многие виды моделей взаимосвязаны. Например, компьютерная модель не может быть без математической. Особая роль отводится математической модели, как одному из строгих и точных методов обоснования проводимых исследований в различных областях деятельности человека, что подтверждается многочисленными публикациями. Вторым важным моментом является тот факт, что только математическая модель позволяет получать прогнозы, качество которых напрямую зависит от качества самой математической модели. Таким образом мы приходим к следующему понятию - показателя качества математической модели, который во многом зависит от основы математической модели.
Приведем классификацию математических моделей в зависимости от ее основы:
1. Математическая модель балансовых задач
2. Математическая модель линейной торговли
|
|
|
3. Математическая модель распределительных задач
4. Математическая модель оптимизационных задач
5. Математическая модель статистических задач
6. Математическая модель в расчетах строительных конструкций.
Математическая модель балансовых задач
Балансовые задачи встречаются в разных областях, например, в природе, производственной сфере. Отсутствие баланса приводит к кризису катастрофам. Имея математическую модель подобной задачи, можем предотвращать негативные процессы. Рассмотрим один из вариантов балансовой задачи – модель межотраслевого баланса, модель Леонтьева
,
где X – объем валового выпуска продукции состоит из объёма производственного потребления - AX и объема конечного потребления - Y. Математическая модель позволяет рассчитать объем конечного потребления – Y, если известен объём валового выпуска
.
Также можно решить более сложную задачу, определить новый объём валового выпуска по заданному новому объёму конечного потребления. Для этого необходимо матричное уравнение решить относительно X. После ряда преобразований, получаем
.
Следует отметить, что эти решения имеют смысл только в случае, когда матрица прямых затрат A является продуктивной. Элементы этой матрицы рассчитываются по формуле
,
где 
- объём продукции производимой отраслью с индексом i и потребляемой отраслью с индексом j при производстве своей продукции объёмом 
. Для определения продуктивности матрицы прямых затрат существуют следующие критерии:
1. Матрица А продуктивна тогда и только тогда, когда матрица 
существует и ее элементы неотрицательны.
2. Матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходят единицы
,
причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы. Элементы матрицы А,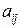 
рассчитываются по формуле
|
|
|
, где i = 1,…, n, j = 1,…, n.
Схему расчетов можно провести в Excel, учитывая особенность работы с цифровой и символьной информацией в Excel. Исходная информация представляется в следующей таблице
Таблица 1
Исходная информация
| Номер отрасли | Объём потребл. отрасли 1 | Объём потребл. отрасли 2 | Объём потребл. отрасли 3 | Объём потребл. отрасли 4 | Объём конечного потреблен. отрасли Y | Объём валого выпуска отрасли X |
| Отрасль №1 | ||||||
| Отрасль №2 | ||||||
| Отрасль №3 | ||||||
| Отрасль №4 |
Таблица 2
Модель межотраслевого баланса с расчетами
| Номер отрасли | Объём потребл. отрасли 1 | Объём потребл. отрасли 2 | Объём потребл. отрасли 3 | Объём конечного потреблен. отрасли Y | Объём валового выпуска отрасли X |
| Отрасль №1 | 5 | 35 | 20 | 40 | 100 |
| Отрасль №2 | 10 | 10 | 20 | 60 | 100 |
| Отрасль №3 | 20 | 10 | 10 | 10 | 50 |
Составим матрицу прямых затрат А, объем валового выпуска X и объем конечного потребления Y
, 
, .
Матрица 
удовлетворяет критериям продуктивности. Для нового объема конечного потребления
новый объем валового выпуска получаем из формулы
.
Рассчитываем матрицу 
:
.
Вычисления произведены с точностью до третьего знака после запятой. Тогда
.
Новый объем конечного потребления 
требует увеличения объема валового выпуска для 1-й отрасли на 52,2 единицы, для 2-й отрасли — на 35,8 единицы, для 3-й отрасли — на 42,5 единицы.
Сравнение величины затрат каждой отрасли на дополнительный объем валового выпуска и прибыли от реализации соответствующего объема конечного продукта дает ответ на вопрос о эффективности нового плана объема конечного потребления.
|
|
|
