 |
Математическая модель статистических задач
|
|
|
|
Очень часто во многих областях встречаются явления, процессы, которые сопровождаются двумя наборами значений. Первый набор значений соответствует исходной информации, а второй набор соответствует результату исследуемого процесса или явления. Математическая модель подобных явлений и процессов является их образом, и позволяет получить о них дополнительную информацию, в том числе и прогноз. Введем определения.
Определение. Данные, характеризующие объект и не меняющиеся со временем, назовем пространственными.
Определение. Данные, характеризующие объект и меняющиеся со временем, назовем временными рядами.
Отметим, что данная классификация не является абсолютной. Они взаимосвязаны, каждая категория данных может переходит из одного вида в другой. Математическая модель пространственных данных основана на уравнениях регрессионного анализа (линейных и нелинейных, однофакторных и многофакторных). Построение регрессионного уравнения основано на методе наименьших квадратов, минимизации отклонений модели от исходной информации. Математическая модель временных рядов более сложна и основана на уравнениях, составной частью которых является основа математической модели пространственных данных. Виды уравнений в зависимости от структуры 1) аддитивная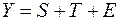 
, 2) мультипликативная: 
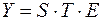, где Y – величина, характеризующая временной ряд, S - циклическая компонента временного ряда, T - трендовая компонента временного ряда, E – случайная компонента временного ряда. Математические модели сопровождаются параметрами: 1) статистическим критерием значимости модели, 2) критерием качества модели. Величина стандартной ошибки для доверительного интервала прогнозируемого значения основано на дисперсионном анализе. Выбор структуры модели временного ряда связано с анализом параметров циклической компоненты. Если частота и амплитуда циклической компоненты стабильны, то предпочтение имеет аддитивная структура модели временного ряда, иначе выбирается мультипликативная модель для временного ряда.
|
|
|
Математическая модель в расчетах строительных конструкций
Пусть задан функционал
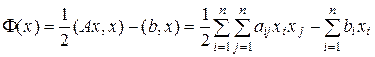, (7)
где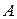 
– симметричная и положительно определенная матрица 
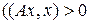при всех 
), 
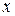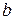– заданный вектор.
Требуется найти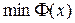 
на множестве векторов .
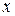Условие минимума функционала (минимума функции нескольких переменных) имеет вид:
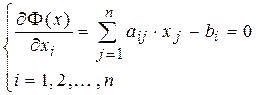или 
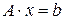(8)
Решение (8) является точкой минимума функционала (7), то есть существует взаимно однозначное соответствие между задачей о минимуме функционала и решением системы линейных уравнений с симметричной матрицей.
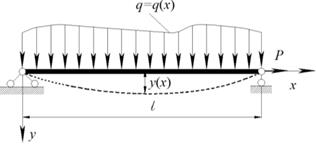
Вариационная постановка задачи об изгибе
Растянуто-изогнутой балки
Из раздела математики «Вариационное исчисление» следует, что задача об изгибе растянуто-изогнутой балки может быть представлена задачей на минимум следующего функционала [7]:
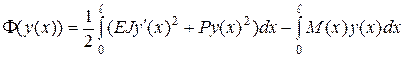, (9)
где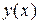 
– функция прогиба балки, 
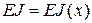– жесткость балки, 
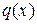– заданная нагрузка на балку, 
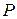– заданная осевая сила, 
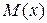– изгибающий момент в балке (известен, поскольку балка статически определимая), 
– длина балки.
Задача состоит в определении функции 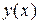, для которой функционал 
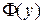принимает минимальное значение (
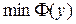). При этом функция 
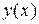должна удовлетворять дополнительному условию 
– шарнирное опирание.
Из курса «Вариационное исчисление» следует, что такая задача на минимум эквивалентна следующей краевой задаче:
Большинству технических задач, как правило, также соответствуют две эквивалентные постановки: вариационная (задача на минимум функционала) и краевая (представленная дифференциальным уравнением и краевыми условиями), имеющих одно и то же решение. По целому ряду соображений вариационная постановка предпочтительнее, поскольку она приводит к более простым и универсальным алгоритмам решения.
|
|
|
|
|
|
