 |
Распределение оценок коэффициентов линейной регрессии
|
|
|
|
При условии нормального распределения вектора 
вектор b подчиняется (k +1)-мерному нормальному закону распределения, как линейная функция нормально распределенного вектора ε. Закон распределения b зависит от вектора математических ожиданий Mb и ковариационной матрицы 
. Так как матрица X постоянна (по условию элементы матрицы X — неслучайные величины), то получим:
.
Мы доказали несмещенность оценок метода наименьших квадратов.
В случае линейной модели вектор b является несмещенной оценкой с минимальной дисперсией вектора 
.
Ковариационная матрица вектора b равна:
= 
Рассмотрим статистический смысл элементов этой матрицы. На главной диагонали матрицы находятся дисперсии элементов вектора оценок b. Вне главной диагонали ковариационной матрицы расположены значения коэффициентов ковариации. Например, на пересечении l -строки и j -го столбца матрицы расположен коэффициент ковариации
,
где 
.
Таким образом, оценка bj коэффициента линейной регрессии 
есть линейная функция от ε. Она имеет нормальный закон распределения с математическим ожиданием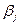 
и дисперсией согласно
,
где 
— диагональный элемент обратной матрицы 
соответствующий j -й строке и j -му столбцу, где 
.
Найдем несмещенную оценку 
для остаточной дисперсии 
, рассмотрим вектор остатков 
.
,
и
.
Тогда
Исходя из того, что произведение 
на обратную 
дает единичную матрицу, последнее слагаемое преобразуется к виду
.
Таким образом,
.
Учитывая, что скалярное произведение векторов 
и 
для всех 
, будем иметь:
.
Легко убедиться, что матрица 
является симметричной, т. е. 
. Для этого достаточно учесть, что
|
|
|
.
Из симметричности матрицы С следует:
,
где i, j = 1,2,...,п.
Принимая во внимание, что математическое ожидание суммы равно сумме математических ожиданий и что элементы матрицы С являются неслучайными величинами, получим:
.
Так как 
по условию, 
при 
, что следует из взаимной независимости величин 
, и 
— след матрицы С, равный сумме диагональных элементов квадратной матрицы.
Подставив вместо С его выражение, получим
.
Здесь учитывается свойство следа матрицы 
; 
— единичная матрица размерности 
. Сумма ее диагональных элементов равна 
, т. е. 
.
Получаем:
.
и несмещенная оценка остаточной дисперсии 
равна:
,
так как 
.
Проверка значимости уравнения регрессии
Для проверки значимости уравнения регрессии воспользуемся F -критерием
Предполагается, что вектор 
имеет нормальный закон распределения
.
Предварительно докажем, что
.
Преобразуем правую часть
Так как величина 
есть скалярная величина, то 
. 
есть сумма квадратов отклонений 
от нуля.
Первое слагаемое 
есть сумма квадратов отклонений результатов наблюдения от регрессии 
. Второе слагаемое 
есть сумма квадратов отклонений от нуля, обусловленных регрессией. Таким образом, Qобщ = QR + Q ОCT - мы имеем разложение общей вариации на составляющие.
Так как ранг п квадратической формы равен сумме рангов (k+1)и (п-k-1) квадратических форм QR и Q ОCT, то согласно теореме Кохрана слагаемые правой части QR и Q ОCT независимы. Откуда
Определим теперь математическое ожидание второго слагаемого QR:
.
Имеем, что
Если предположить, что 
, где 0 — нулевой вектор, то 
, откуда 
. Мы показали, что при выполнении условия 
, т. е. когда 
, 
и 
являются независимыми и несмещенными оценками одной и той же дисперсии .
В этой связи для проверки гипотезы Н0: 
используется статистика
,
которая при выполнении гипотезы Н0 имеет F -распределение с (k+1)и (п-k-1) степенями свободы.
|
|
|
Если уравнение регрессии незначимо, т. е. все коэффициенты уравнения регрессии для генеральной совокупности равны нулю, то на этом анализ уравнения регрессии заканчивается.
Если же нулевая гипотеза Н0: 
отвергается, то представляет интерес проверка значимости отдельных коэффициентов регрессии и построение интервальных оценок для значимых коэффициентов.
Значимость коэффициентов регрессии, т. е. гипотезу Н0: 
, можно проверить с помощью t -критерия, основанного на статистике
,
где l = j + 1, которая при выполнении гипотезы Н0: 
имеет t -распределение с числом степеней свободы п-k-1.
|
|
|
