 |
Простейшая линейная модель регрессии
|
|
|
|
Оценивание параметров регрессии
Пусть на основании анализа исследуемого явления предполагается, что в среднем у есть линейная функция от х, т. е. имеет место уравнение регрессии

где  — условное математическое ожидание случайной величины у при заданном х. Объясняющая переменная х рассматривается как неслучайная величина;
— условное математическое ожидание случайной величины у при заданном х. Объясняющая переменная х рассматривается как неслучайная величина;
 и
и  — неизвестные параметры генеральной совокупности, которые подлежат оценке по результатам выборочных наблюдений.
— неизвестные параметры генеральной совокупности, которые подлежат оценке по результатам выборочных наблюдений.
Предположим, что для оценки параметров  и
и  из двухмерной генеральной совокупности (х, у) взята выборка объемом и, где
из двухмерной генеральной совокупности (х, у) взята выборка объемом и, где  результат i -го наблюдения (i =1,2,..., п). В этом случае линейная модель регрессии имеет вид
результат i -го наблюдения (i =1,2,..., п). В этом случае линейная модель регрессии имеет вид
 ,
,
где  — взаимно независимые случайные величины с нулевым математическим ожиданием и дисперсией
— взаимно независимые случайные величины с нулевым математическим ожиданием и дисперсией  , т. е.
, т. е.  для всех i =1,2,..., п и
для всех i =1,2,..., п и 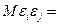
 при i = j -(условие гомоскедастичности, постоянства остаточной дисперсии;) и равными 0 при i ≠ j -(условие взаимной некоррелированности регрессионных остатков.)
при i = j -(условие гомоскедастичности, постоянства остаточной дисперсии;) и равными 0 при i ≠ j -(условие взаимной некоррелированности регрессионных остатков.)
Согласно методу наименьших квадратов в качестве оценок неизвестных параметров  и
и  , следует брать такие значения выборочных характеристик b0 и b1, которые минимизируют сумму квадратов отклонений значений результативного признака yt от условного математического ожидания
, следует брать такие значения выборочных характеристик b0 и b1, которые минимизируют сумму квадратов отклонений значений результативного признака yt от условного математического ожидания  , т. е.
, т. е.

Так как Q дифференцируема по  и
и  , то для отыскания минимума функции найдем частные производные по
, то для отыскания минимума функции найдем частные производные по  и
и  :
:
 .
.
Приравняв производные нулю и подставив вместо  и
и  их оценки b0 и b1, получим:
их оценки b0 и b1, получим:
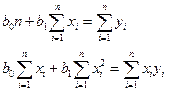
Данная система уравнений называется системой нормальных уравнений. Решая систему относительно b0 и b1получим:

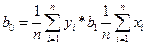
Перейдя к средним, будем иметь
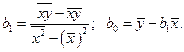
Докажем, что в случае нормального закона распределения случайной величины  , а отсюда и
, а отсюда и  , оценки метода наименьших квадратов и наибольшего правдоподобия совпадают.
, оценки метода наименьших квадратов и наибольшего правдоподобия совпадают.
|
|
|
Пусть из двумерной генеральной совокупности (х, у) взята независимая выборка  , где i = 1, 2,..., п, объемом n.
, где i = 1, 2,..., п, объемом n.
Будем рассматривать у i, как независимые нормальные случайные величины с математическим ожиданием  , являющимся функцией от xi, и постоянной дисперсией
, являющимся функцией от xi, и постоянной дисперсией  .
.
Тогда  , где
, где  , и функция правдоподобия примет вид с учетом независимости наблюдения
, и функция правдоподобия примет вид с учетом независимости наблюдения
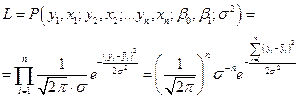
Согласно методу наибольшего правдоподобия в качестве оценок параметров  и
и  возьмем значения
возьмем значения  и
и  , максимизирующие L. При заданных
, максимизирующие L. При заданных  и постоянном
и постоянном  функция правдоподобия L достигнет максимума, когда показатель степени при е будет минимальным, т. е. при условии минимума функции
функция правдоподобия L достигнет максимума, когда показатель степени при е будет минимальным, т. е. при условии минимума функции  , что совпадает с условием нахождения оценок
, что совпадает с условием нахождения оценок  по методу наименьших квадратов. Таким образом, оценки
по методу наименьших квадратов. Таким образом, оценки  обладают свойствами оценок наибольшего правдоподобия.
обладают свойствами оценок наибольшего правдоподобия.
Однако функция правдоподобия L зависит также и от параметра  . Из условия
. Из условия  найдем оценку
найдем оценку  наибольшего правдоподобия параметра
наибольшего правдоподобия параметра  :
:

Несмещенная оценка параметра  равна
равна

Исследуем свойства  и
и  .
.
Определение интервальной оценки для Р0
Будем рассматривать модель регрессионного анализа
 или
или  ,
,
где 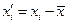 — центрированные величины, удовлетворяющие условию
— центрированные величины, удовлетворяющие условию
 .
.
Тогда оценки  и
и  метода наименьших квадратов равны
метода наименьших квадратов равны

Но

Откуда получим:

Величина  есть линейная функция нормальных случайных величин
есть линейная функция нормальных случайных величин  . Следовательно, она также имеет нормальный закон распределения с математическим ожиданием
. Следовательно, она также имеет нормальный закон распределения с математическим ожиданием

так как по условию  , и дисперсией
, и дисперсией

Здесь учитывалось, что  , взаимонезависимые случайные величины с дисперсией
, взаимонезависимые случайные величины с дисперсией  для всех i = 1, 2,…,п.
для всех i = 1, 2,…,п.
Подставляя вместо  несмещенную оценку
несмещенную оценку  , получим оценку дисперсии
, получим оценку дисперсии  , для
, для  ,
,  .
.
Таким образом,  есть случайная величина, имеющая нормальный закон распределения
есть случайная величина, имеющая нормальный закон распределения  .
.
Отсюда следует, что величина
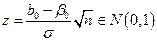
имеет нормированный нормальный закон распределения.
|
|
|
С другой стороны, статистика

имеет  - распределение с
- распределение с 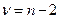 степенями свободы, так как уравнение регрессии определяется двумя параметрами
степенями свободы, так как уравнение регрессии определяется двумя параметрами  и
и  , которые подлежат оцениванию.
, которые подлежат оцениванию.
Отсюда следует, что статистика

имеет t -распределение Стьюдента с 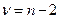 степенями свободы.
степенями свободы.
С помощью статистики t построим с доверительной вероятностью  интервальную оценку для
интервальную оценку для  из условия
из условия

Откуда получим:

или, учитывая, что  , будем иметь:
, будем иметь:  , где
, где  определяется по таблице распределения Стьюдента (t -распределение) для уровней значимости
определяется по таблице распределения Стьюдента (t -распределение) для уровней значимости  и числа степеней свободы (
и числа степеней свободы (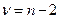 ).
).
Определение интервальной оценки и проверка значимости β1
Рассмотрим выражение

Решив уравнение относительно  получим:
получим:
 ,
,
откуда будем иметь:
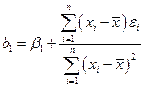
Это значит, что  есть линейная функция независимых нормально распределенных случайных величин
есть линейная функция независимых нормально распределенных случайных величин  , где
, где  . Следовательно, она также имеет нормальный закон распределения.
. Следовательно, она также имеет нормальный закон распределения.
Определим математическое ожидание и дисперсию  .
.
Учитывая, что математическое ожидание суммы равно сумме математических ожиданий, что неслучайный множитель 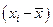 можно вынести за знак математического ожидания и
можно вынести за знак математического ожидания и  , получим:
, получим:

Так как  есть независимые между собой случайные величины с дисперсией
есть независимые между собой случайные величины с дисперсией  , а дисперсия постоянной величины равна нулю, т. е.
, а дисперсия постоянной величины равна нулю, т. е.  , то
, то

откуда получим

Мы доказали, что в  есть случайная величина, имеющая нормальный закон распределения:
есть случайная величина, имеющая нормальный закон распределения:

Отсюда следует, что
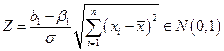
Учитывая независимость случайных величин, получим статистику, имеющую t -распределение c (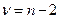 ) степенями свободы:
) степенями свободы:

Интервальную оценку для  с надежностью у найдем из условия:
с надежностью у найдем из условия:  .
.
После преобразования) получим:
 ,
, 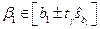 ,
,
где  находят по таблице t -распределения при
находят по таблице t -распределения при  и
и  ;
;
 — несмещенная оценка дисперсии Db 1;
— несмещенная оценка дисперсии Db 1;
 — оценка среднего квадратического отклонения величины b 1.
— оценка среднего квадратического отклонения величины b 1.
Интервальную оценку с надежностью  для
для  найдем с помощью статистики
найдем с помощью статистики  ,
,
где  находят по таблице
находят по таблице  - распределения для числа степеней свободы (
- распределения для числа степеней свободы (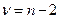 ) и вероятностей соответственно
) и вероятностей соответственно  и
и  .
.
Установление значимости простейшего линейного уравнения регрессии  сводится к проверке при заданном
сводится к проверке при заданном  нулевой гипотезы о значимости коэффициента регрессии
нулевой гипотезы о значимости коэффициента регрессии  т. е. гипотезы Н0:
т. е. гипотезы Н0:  при альтернативной гипотезе Hl:
при альтернативной гипотезе Hl:  .
.
|
|
|
С этой целью используется t -критерий, и значение статистики критерия  сравнивают с критическим значением
сравнивают с критическим значением 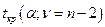 , найденным по таблице t -распределения при заданном
, найденным по таблице t -распределения при заданном  и
и 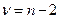 .
.
Гипотеза Н0:  отвергается с вероятностью ошибки
отвергается с вероятностью ошибки  при выполнении неравенства
при выполнении неравенства 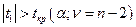 и уравнение регрессии считается значимым. В противном случае, т.е. если
и уравнение регрессии считается значимым. В противном случае, т.е. если  , гипотеза Н0:
, гипотеза Н0:  не отвергается и уравнение регрессии считают незначимым и на этом регрессионный анализ заканчивается.
не отвергается и уравнение регрессии считают незначимым и на этом регрессионный анализ заканчивается.
Для значимого уравнения регрессии представляет интерес построение интервальных оценок для коэффициента регрессии  свободного члена
свободного члена  и самого уравнения
и самого уравнения 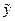 .
.
Определение интервальной оценки для условного математического ожидания
Пусть имеем уравнение регрессии

и его оценку

где  — оценки метода наименьших квадратов параметров уравнения
— оценки метода наименьших квадратов параметров уравнения  .
.
Величина  есть линейная функция двух случайных величин
есть линейная функция двух случайных величин  и
и  имеющих нормальный закон распределения. Следовательно,
имеющих нормальный закон распределения. Следовательно,  также имеет нормальный закон распределения. Определим параметры этого закона. Получим:
также имеет нормальный закон распределения. Определим параметры этого закона. Получим:
 .
.
Откуда  .
.
Для определения дисперсии  предварительно докажем независимость величин
предварительно докажем независимость величин  и
и  .
.
Так как величины  и
и  имеют нормальный закон распределения, то независимость этих величин следует из их некоррелированности. Следовательно, нам достаточно доказать, что
имеют нормальный закон распределения, то независимость этих величин следует из их некоррелированности. Следовательно, нам достаточно доказать, что
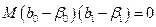 .
.
Учитывая, что х, есть неслучайная величина, получим:

Так как 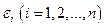 по условию есть независимые случайные величины с
по условию есть независимые случайные величины с  , то
, то  при
при  , где
, где  . Следовательно,
. Следовательно,
 ,
,
где  . Учитывая, что
. Учитывая, что  , после подстановки окончательно получим:
, после подстановки окончательно получим:
 .
.
Этот результат получен для центрированных величин  , для которых выполняется условие
, для которых выполняется условие  . В этом случае
. В этом случае  и
и  — независимые случайные величины. Тогда согласно выражению (2.26), дисперсия величины
— независимые случайные величины. Тогда согласно выражению (2.26), дисперсия величины  равна сумме дисперсий слагаемых, т.е.
равна сумме дисперсий слагаемых, т.е.
 .
.
Получаем:

Таким образом,

Тогда нормированный нормальный закон распределения имеет величина
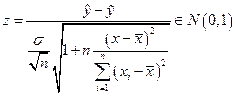 .
.
Откуда получим выборочную характеристику
 ,
,
которая имеет распределение Стьюдента (t -распределение) с (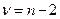 ) степенями свободы.
) степенями свободы.
|
|
|
Тогда с надежностью  доверительный интервал для
доверительный интервал для  при заданном х = х 0 равен
при заданном х = х 0 равен
 ,
,
где  определяется по таблице распределения Стьюдента для уровня значимости
определяется по таблице распределения Стьюдента для уровня значимости  и (
и (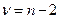 ) числа степеней свободы.
) числа степеней свободы.
Интервальная оценка для прогнозного значения у в точке  , определяется как
, определяется как
 .
.
У прогнозного значения уп+1 дисперсия на  больше, чем у величины
больше, чем у величины  на величину дисперсии.
на величину дисперсии.
По мере удаления х0 от среднего значения ( ) ширина доверительного интервала увеличивается, а точность оценки
) ширина доверительного интервала увеличивается, а точность оценки 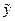 снижается. Доверительный интервал имеет наименьшую величину, когда
снижается. Доверительный интервал имеет наименьшую величину, когда  , т. е. наблюдаемое значение признака равно
, т. е. наблюдаемое значение признака равно  . Расположение доверительного интервала для
. Расположение доверительного интервала для  , найденного с надежностью
, найденного с надежностью  , иллюстрирует рис. 2.1.
, иллюстрирует рис. 2.1.

Рис. 2.1. Расположение доверительных границ в случае линейной регрессии
2.1.2. Применение методов многофакторного регрессионного анализа в задачах строительства
Методы многофакторного регрессионного анализа находят широкое применение в задачах строительства. Так регрессионный анализ позволяет установить соответствие между ценой объекта недвижимости с учётом влияющих на её цену факторов, при организации строительного производства - учесть влияние внутренних и внешних факторов, влияющих на эффективность производственной деятельности, при принятии управленческих решений -провести сравнение различных технологий и принять оптимальное решение.
Рассмотрим общий случай линейной зависимости, когда результативный показатель у с точностью до случайной составляющей ε есть линейная функция от k объясняющих переменных х1,х2,…,хk.
Пусть из (k + 1)-мерной генеральной совокупности (у, х1, х2,…,хk) взята случайная выборка объемом и пусть i-е наблюдение имеет вид (yi,хi1,хi2,..,xik), где i = 1,2,…,п.
Под КЛММР будем понимать регрессионную модель вида  , для всех i =1,2,..., п, где
, для всех i =1,2,..., п, где  — неизвестные параметры модели, подлежащие оцениванию по выборке, есть неслучайные величины, как параметры генеральной совокупности.
— неизвестные параметры модели, подлежащие оцениванию по выборке, есть неслучайные величины, как параметры генеральной совокупности.
Объясняющие переменные и регрессионные остатки модели удовлетворяют требованиям:
а) объясняющие переменные х1,х2,…,хk рассматриваются как неслучайные величины, т. е. предполагается, что они измерены без ошибок;
б) величины х1,х2,…,хk не связаны между собой линейной функциональной зависимостью;
в) регрессионные остатки ε i есть взаимонезависимые случайные вели-
чины с нулевым математическим ожиданием  и дисперсией равной:
и дисперсией равной:  для всех i = 1,2,..., п. Отсюда следует, что коэффициент ковариации
для всех i = 1,2,..., п. Отсюда следует, что коэффициент ковариации
 ,
,
где i, l =1,2,..., п;
г) при анализе свойств оценки уравнения регрессии обычно исходят
из того, что вектор  регрессионных остатков подчиняется
регрессионных остатков подчиняется
n -мерному нормальному закону распределения с вектором математических ожиданий  и ковариационной матрицей
и ковариационной матрицей  , т. е.
, т. е.  , где
, где  — единичная матрица размерности п*п.
— единичная матрица размерности п*п.
|
|
|
Найдем математическое ожидание yi при заданном векторе значений объясняющих переменных  .Получим:
.Получим:
 .
.
Мы получили уравнение регрессии, характеризующее функциональную зависимость среднего значения у от объясняющих переменных 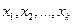 .
.
В этом уравнении  называют свободным членом уравнения. Обычно он содержательно не интерпретируется, так как в экономике случай, когда все объясняющие переменные
называют свободным членом уравнения. Обычно он содержательно не интерпретируется, так как в экономике случай, когда все объясняющие переменные 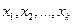 равны нулю, так как не имеет содержательного смысла. Например, в регрессионной модели производительности труда о каком производстве может идти речь, если равны нулю производственные площади, число работающих и т. д.
равны нулю, так как не имеет содержательного смысла. Например, в регрессионной модели производительности труда о каком производстве может идти речь, если равны нулю производственные площади, число работающих и т. д.
Параметры модели  называются коэффициентами регрессии. Коэффициент регрессии
называются коэффициентами регрессии. Коэффициент регрессии 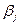 показывает, на какую величину в среднем изменится у, если переменную хj, увеличить на единицу при неизменных значениях остальных объясняющих переменных, входящих в модель. Это легко проверить, если, например, в (3.3) к хik прибавить единицу. Будем иметь:
показывает, на какую величину в среднем изменится у, если переменную хj, увеличить на единицу при неизменных значениях остальных объясняющих переменных, входящих в модель. Это легко проверить, если, например, в (3.3) к хik прибавить единицу. Будем иметь:
 .
.
В матричной форме линейная модель имеет вид
 ,
,
где  — вектор-столбец (размерности п) значений результативного показателя;
— вектор-столбец (размерности п) значений результативного показателя;
 — матрица (размерности п*(к+1)) значений объясняющих переменных;
— матрица (размерности п*(к+1)) значений объясняющих переменных;
 — вектор– столбец (размерности (k +1)) неизвестных параметров, которые подлежат оцениванию по выборке;
— вектор– столбец (размерности (k +1)) неизвестных параметров, которые подлежат оцениванию по выборке;
 — вектор – столбец (размерности n) случайных ошибок, регрессионных остатков.
— вектор – столбец (размерности n) случайных ошибок, регрессионных остатков.
Причем  ,
,
где 0 – вектор – столбец, все n значений которого равны 0, а ковариационная матрица
 .
.
Из условия (3.2) следует, что для i = 1, 2,…, п  и
и  при
при  тогда
тогда
 ,
,
где  — единичная матрица размерности (n × n).
— единичная матрица размерности (n × n).
|
|
|


