 |
Однофакторный дисперсионный анализ
|
|
|
|
Простейшим случаем дисперсионного анализа является однофакторный анализ. В этой главе мы дадим его определение и будем использовать этот случай для иллюстрации некоторых положений общей теории оценок и критериев, изложенной далее. Кроме того, будут введены также некоторые новые понятия и методы, относящиеся к задачам множественного сравнения (построение некоторых видов совместных доверительных интервалов и соответствующих им критериев). Сначала эти понятия и методы вводятся в связи с классификацией по одному признаку, а затем будут перенесены на общий случай. После этого мы сможем рассматривать эти методы как дополнение общего F -критерия гл. 2 в следующем смысле. Мы видели, что нулевая гипотеза Н равносильна утверждению, что все параметрические функции некоторого класса имеют нулевые значения. Каждый раз, когда по F -критерию Н отвергается, мы можем одним из методов множественного сравнения решить, какая параметрическая функция рассматриваемого класса отличается от нуля и как велико это отличие. Мы увидим также, что F -критерий можно рассматривать как предварительный метод решения вопроса о целесообразности продолжения обработки наблюдений другими более сложными методами, или F -критерий можно применить к исследованию оценки функции из рассматриваемого класса, которая в некотором смысле сильно отличается от нуля, и решить, значимо ли отличается от нуля эта оценка.
Термин однофакторный анализ (или классификация по одному признаку) относится к сравнению средних нескольких (одномерных) популяций. Обозначим их средние через  . Допустим, что популяции нормально распределены с равными дисперсиями
. Допустим, что популяции нормально распределены с равными дисперсиями  . Пусть мы имеем независимые выборки объемов
. Пусть мы имеем независимые выборки объемов  из соответствующих популяций. Обозначим выборку из i-й популяции через
из соответствующих популяций. Обозначим выборку из i-й популяции через  - Тогда наши основные предположения равносильны следующим:
- Тогда наши основные предположения равносильны следующим:
|
|
|

Используя общую теорию для проверки гипотезы
Н:  ,
,
мы построим F -критерий в предположениях  . Обозначение вектора наблюдений
. Обозначение вектора наблюдений  используемое в общей теории, нужно заменить обозначением с двойными индексами координат, а именно
используемое в общей теории, нужно заменить обозначением с двойными индексами координат, а именно  . Из равенств
. Из равенств  заключаем, что (n
заключаем, что (n  I)-матрица
I)-матрица  теперь имеет следующий вид: каждая из первых J 1строк равна
теперь имеет следующий вид: каждая из первых J 1строк равна 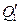 , каждая из следующих J 2 строк равна
, каждая из следующих J 2 строк равна 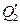 ,..., каждая из последних JI строк равна
,..., каждая из последних JI строк равна  , где
, где  является i -й строкой единичной матрицы. Таким образом, ранг r (число линейно независимых строк) матрицы
является i -й строкой единичной матрицы. Таким образом, ранг r (число линейно независимых строк) матрицы  равен I (числу столбцов
равен I (числу столбцов 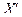 обозначенному в общей теории гл. 1 через р). Отсюда следует, что любая параметрическая функция допускает оценку.
обозначенному в общей теории гл. 1 через р). Отсюда следует, что любая параметрическая функция допускает оценку.
Сумма квадратов 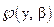 , которую мы должны минимизировать при
, которую мы должны минимизировать при  и
и  , вычисляется по формуле
, вычисляется по формуле
 .
.
Нормальные уравнения в предположениях  можно получить,
можно получить,
приравнивая к нулю производные

при 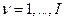 . Уравнения дают мнк -оценки
. Уравнения дают мнк -оценки  . В дальнейшем мы будем часто использовать следующее удобное обозначение. Так мнк -оценки
. В дальнейшем мы будем часто использовать следующее удобное обозначение. Так мнк -оценки  можно записать в виде
можно записать в виде
 .
.
Замена индекса звездочкой показывает, что вычислено арифметическое среднее величин, в которых заменяется индекс, по всем возможным значениям этого индекса. В этих предположениях функцию  можно записать как
можно записать как
 ,
,
где через  обозначено общее (неизвестное) значение величин
обозначено общее (неизвестное) значение величин  . В этом случае имеется только одно нормальное уравнение
. В этом случае имеется только одно нормальное уравнение
 .
.
Из этого уравнения находим (крышка над  указывает, что это оценка неизвестного
указывает, что это оценка неизвестного  )
)

Далее  , где
, где  является мнк -оценкой
является мнк -оценкой  при
при 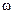 .
.
Для вычисления SS удобно использовать  -обозначения. Будем через
-обозначения. Будем через  обозначать
обозначать  , а через
, а через 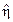 и
и  — мнк -оценки
— мнк -оценки  при
при  и
и 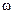 , равные проекциям у на пространства Vr и Vr-q, которым
, равные проекциям у на пространства Vr и Vr-q, которым  принадлежит соответственно при условиях
принадлежит соответственно при условиях  и
и  . Координаты векторов
. Координаты векторов  ,
,  и
и  можно теперь занумеровать двойными индексами по аналогии с координатами у. Тогда «(i, j)-координата» (координата с индексом ij) вектора
можно теперь занумеровать двойными индексами по аналогии с координатами у. Тогда «(i, j)-координата» (координата с индексом ij) вектора  равна
равна  , следовательно,
, следовательно,  и
и  при
при  .
.
|
|
|
Можно получить (i, j)-координату  , заменив
, заменив  на их мнк -оценки при
на их мнк -оценки при  ; эта замена дает
; эта замена дает  .
.
Произведя аналогичную замену при  , найдем, что (i, j)-координата вектора
, найдем, что (i, j)-координата вектора  равна
равна 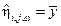 .
.
Суммы квадратов в числителе и знаменателе статистики  мы получаем из общих тождеств
мы получаем из общих тождеств
 ,
,  ,
,
которые преобразуются в
 ,
,
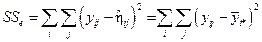 .
.
Эти формулы подсказывают простое наглядное объяснение: SSH представляет собой взвешенную меру разброса выборочного среднего в I популяциях, a SSe является составной мерой разброса наблюдений в пределах каждой из I выборок. По этим соображениям SSH можно назвать SS между группами, a SSe можно назвать SS внутри групп. Для численного вычисления этих SS используются формулы, которые также следуют из общих тождеств. Тождество  в нашем случае имеет вид
в нашем случае имеет вид
 ,
,
 .
.
Общее тождество  или
или  запишется в виде
запишется в виде
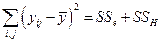 .
.
Сумму квадратов в левой части можно назвать полным SS относительно общего среднего. Обозначать эту сумму будем через SSП в отличие от 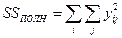 . В этих обозначениях можно записать так:
. В этих обозначениях можно записать так:

Окончательно общее тождество  принимает вид
принимает вид
 .
.
Гипотезу Н можно задать, приравнивая к нулю I -1 различных линейно независимых функций; например,
Н:  .
.
Отсюда число ст. св. SSH равно q = I -1. Мы уже видели, что г= I, так что число ст. св. SSe равно п - r = п - I. Таким
образом, статистикой  является отношение
является отношение  , где
, где
 ,
,  .
.
По F -критерию гипотеза Н отвергается с заданным уровнем значимости  тогда и только тогда, когда
тогда и только тогда, когда  . При
. При  статистика
статистика  имеет нецентральное F -pacпределение, а именно
имеет нецентральное F -pacпределение, а именно  является величиной
является величиной  ,
,
Если мы положим  , так что
, так что

Некоторые из этих результатов собраны в таблицу.
Таблица1
Однофакторный анализ
| Источник дисперсии | 
| Степень свободы | 
| 
|
| Между группами Внутри групп | 

| I-1 n-1 | 

| 

|
| «Полная» сумма квадратов | 
| n-1 | — | — |
Методы вычислений, предложенные в этой книге, облегчаются применением ЭВМ. Весьма часто требуется сохранять большое число верных знаков до конца вычислений из-за возможной потери их при вычислении SS вычитанием из другого SS. Понятно, что в промежуточных вычислениях лучше иметь больше знаков, так как если после вычитания их останется слишком мало, то придется повторить полностью все вычисления. С другой стороны, окончательный результат должен содержать разумное число знаков, обычно такое, чтобы единица последнего сохраненного знака имела порядок пяти оценок стандартного отклонения результата. Статистик, работающий с химиками или инженерами, может дискредитировать себя необдуманным предложением доверительного интервала такого вида 7,32179 ± 0,05248 вместо 7,32 ±0,05 или использованием углового коэффициента прямой с семью знаками, когда сама прямая была подобрана по данным с тремя знаками. При вычислениях с машинами, или без них (особенно если у чисел совпадают знаки старших разрядов), полезно преобразовать данные вычитанием подходящей постоянной; например, если данные заключены в пределах от 151,2 до 158,7, то удобно вычесть 150; результат, вычисленный по преобразованным данным, очевидно, будет такой же, как по исходным.
|
|
|
2.2.2. Многофакторный анализ
В этом параграфе мы применяем общую теорию к простейшим планам эксперимента для исследования эффектов двух факторов. Эти простейшие планы мы будем называть полным анализом. В конце главы будет рассмотрена общая задача разбиения суммы квадратов.
Предположим, что два фактора A и В изменяются в эксперименте или в рассматриваемой совокупности условий, например в эксперименте типа, где различные растения (А) были посажены на различных участках (В) с одинаковым химическим составом смесей, или, например в исследованиях нескольких видов технологий (А), наблюдаемых на различных строительных объектах (В). Если в первом примере рассматривается I растений и J местностей, то эти I и J называют соответственно I уровнями фактора A и J уровнями фактора В. Уровни могут описывать качественную классификацию, как, например, виды растений, или же количественную, как, например, затраты на применение технологии.
В таких двухфакторных экспериментах наблюдения могут быть расположены по этим двум факторам в виде таблицы с двумя входами (двухфакторной таблицы), I строк которой соответствуют уровням фактора A, а J столбцов — уровням В. В «(i, j) -ячейку», расположенную на пересечении i -й строки и j -го столбца, записываются наблюдения, полученные при одновременном исследовании факторов А и В соответственно в i-м и j -м уровнях. Если в каждой ячейке есть по крайней мере одно наблюдение, то возможен полный анализ. Если мы допустим, что наблюдения в (i, j)-ячейке являются случайной выборкой из популяции, соответствующей этой ячейке, то можно говорить о среднем и дисперсии этой популяции как об «истинном» среднем ячейки и «истинной» дисперсии ячейки. Все понятия этого параграфа будут определены в терминах «истинных» средних ячейки, которые также называют «истинными» результатами в рассматриваемой совокупности условий. Мы будем обозначать «истинное» среднее (i, j)-ячейки через  если нет дополнительных предположений относительно {
если нет дополнительных предположений относительно {  }, то мнк -оценкой, как будет показано позднее, является среднее наблюдение в (i, j)-ячейке. Это среднее называют наблюденным средним ячейки или наблюденным результатом. Для краткости мы будем опускать слово «истинный», но везде в этом параграфе будут иметься в виду «истинные» значения.
}, то мнк -оценкой, как будет показано позднее, является среднее наблюдение в (i, j)-ячейке. Это среднее называют наблюденным средним ячейки или наблюденным результатом. Для краткости мы будем опускать слово «истинный», но везде в этом параграфе будут иметься в виду «истинные» значения.
|
|
|
Предположим, что веса  выбраны в соответствии с уровнями фактора В. Например, если в J местностях Калифорнии I сортов хлопка проверяется в эксперименте, на основании которого для всей Калифорнии будет отобран единственный сорт, то естественно взвесить J местностей с весами
выбраны в соответствии с уровнями фактора В. Например, если в J местностях Калифорнии I сортов хлопка проверяется в эксперименте, на основании которого для всей Калифорнии будет отобран единственный сорт, то естественно взвесить J местностей с весами  , пропорциональными площадям хлопка в областях, типичными представителями которых являются эти J местностей. Средним i-го уровня А называют взвешенное среднее от средних ячейки {
, пропорциональными площадям хлопка в областях, типичными представителями которых являются эти J местностей. Средним i-го уровня А называют взвешенное среднее от средних ячейки {  } i -й строки, причем веса
} i -й строки, причем веса  зависят от столбцов и не зависят от строк; таким образом, это среднее является средним результатом i-го уровня A, осредненным по уровням В. Предполагается, что веса
зависят от столбцов и не зависят от строк; таким образом, это среднее является средним результатом i-го уровня A, осредненным по уровням В. Предполагается, что веса  неотрицательны и не все равны нулю, поэтому, не нарушая общности, можно допустить, что
неотрицательны и не все равны нулю, поэтому, не нарушая общности, можно допустить, что 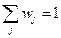 .
.
Таким образом, 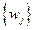 рассматриваются как произвольные, но фиксированные числа. Теперь среднее i-го уровня А запишется в виде
рассматриваются как произвольные, но фиксированные числа. Теперь среднее i-го уровня А запишется в виде  ; это среднее называют также средним i -й строки. Аналогично если
; это среднее называют также средним i -й строки. Аналогично если  является произвольным множеством чисел со всеми
является произвольным множеством чисел со всеми  и
и  , то среднее j-го уровня B, или среднее j-го cтолбца, определяется формулой
, то среднее j-го уровня B, или среднее j-го cтолбца, определяется формулой
 ,
,
Генеральным средним будем называть взвешенное среднее средних столбца {В j } с весами  , или взвешенное среднее средних строки {Ai} с весами
, или взвешенное среднее средних строки {Ai} с весами  . Обозначая генеральное среднее через
. Обозначая генеральное среднее через  , получим
, получим
 .
.
Главный эффект i-го уровня А определяется как превышение среднего i -го уровня над генеральным средним
|
|
|
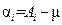 .
.
Отметим, что {  } удовлетворяют условию
} удовлетворяют условию  .
.
Аналогично главный эффект j -го уровня В определяется как
 ,
,
откуда
 .
.
Главные эффекты  и
и  называют также эффектом i-й строки и эффектом j-го столбца. Мы придаем особое значение тому, что главные эффекты одного фактора являются средними по уровням других факторов и, таким образом, обычно зависят от того, каковы уровни других факторов, присутствующих в эксперименте (когда используется модель с фиксированными факторами, рассматриваемая в первой части книги).
называют также эффектом i-й строки и эффектом j-го столбца. Мы придаем особое значение тому, что главные эффекты одного фактора являются средними по уровням других факторов и, таким образом, обычно зависят от того, каковы уровни других факторов, присутствующих в эксперименте (когда используется модель с фиксированными факторами, рассматриваемая в первой части книги).
Если мы будем определять главный эффект i -го уровня А специально по отношению к j -му уровню В, то естественно определить его как превышение  над средним j -го столбца, т. е.
над средним j -го столбца, т. е.  .
.
Главный эффект i -го уровня A, определенный выше, является фактически взвешенным средним от по столбцам:  . Превышение над своим средним называется взаимодействием i-го уровня А с j-м уровнем В
. Превышение над своим средним называется взаимодействием i-го уровня А с j-м уровнем В  .
.
Мы могли бы прийти к тому же результату, если бы начали с главного эффекта j -го уровня В специально по отношению к i -му уровню А; взаимодействие симметрично, поэтому мы можем назвать  взаимодействием i -го уровня А и j -го уровня В. Отметим, что IJ взаимодействий удовлетворяют условиям
взаимодействием i -го уровня А и j -го уровня В. Отметим, что IJ взаимодействий удовлетворяют условиям
 ; при всех j;
; при всех j;
 ; при всех i.
; при всех i.
Подставляя  и
и  получим
получим  .
.
Предположим, что 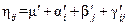 .Вычисляя
.Вычисляя  ,
,  ,
,  и
и  по их определениям через
по их определениям через  и допуская, что первоначальные величины удовлетворяют дополнительным условиям, мы получим
и допуская, что первоначальные величины удовлетворяют дополнительным условиям, мы получим  .
.
Теорема. Если при некоторой системе весов  и
и  все взаимодействия
все взаимодействия  равны нулю, то все они равны нулю при любой другой системе весов. В этом случае каждое сравнение главных эффектов
равны нулю, то все они равны нулю при любой другой системе весов. В этом случае каждое сравнение главных эффектов 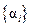 или
или 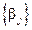 имеет значение, не зависящее от системы весов
имеет значение, не зависящее от системы весов  и
и 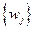 ; такое же утверждение верно для сравнений средних {Ai} и { В j } уровней А и В соответственно.
; такое же утверждение верно для сравнений средних {Ai} и { В j } уровней А и В соответственно.
Доказательство. При некоторой частной системе весов  и
и  определенные выше величины
определенные выше величины  обозначим через
обозначим через  . Предположим, что все
. Предположим, что все 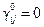 .
.
 .
.
Пусть теперь 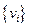 и
и  —любая другая система весов, так что
—любая другая система весов, так что  ,
,  ,
,  ,
,  .Тогда получим
.Тогда получим
 ,
,
и аналогично
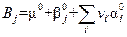 ,
,
 .
.
Подставляя эти три выражения мы найдем, что 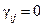 . Это доказывает теорему.
. Это доказывает теорему.
Мы говорим о случае отсутствия взаимодействий, если все 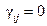 . Из доказанной выше теоремы следует, что при другой системе весов мы тоже получим случай отсутствие взаимодействий. Из этой же теоремы следует, что значения всх сравнений главных эффектов
. Из доказанной выше теоремы следует, что при другой системе весов мы тоже получим случай отсутствие взаимодействий. Из этой же теоремы следует, что значения всх сравнений главных эффектов  и
и  не изменятся, если даже вычислять
не изменятся, если даже вычислять  и
и  с различными весами. Случай отсутствия взаимодействий называют также случаем аддитивности эффектов. Формально его можно определить как существования постоянных {ai}, {bj} таких, что
с различными весами. Случай отсутствия взаимодействий называют также случаем аддитивности эффектов. Формально его можно определить как существования постоянных {ai}, {bj} таких, что  при всех (i, j); тогда так же, как в доказательстве приведенной выше теоремы, отсюда легко следует, что все
при всех (i, j); тогда так же, как в доказательстве приведенной выше теоремы, отсюда легко следует, что все 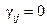 .
.
Интерпретация дисперсионного анализа является очень простой, когда мы решаем (на основании статистических или других соображений), что взаимодействия отсутствуют. Тогда нашими заключениями о главных эффектах (и, возможно, о генеральном среднем) обычно достаточно суммировать весь анализ. Так, например, если мы сравниваем первую разновидность растений со второй (в примере с растениями и участками) и заключаем, что сравнение (главный эффект первой разновидности) — (главный эффект второй разновидности) положительно, то из этого вытекает, что первая разновидность лучше второй в одном и том же смысле для всех местностей; но если мы не сделали предположения об аддитивности эффектов, то наше заключение может быть таким: среднее по J местностям первой разновидности лучше среднего второй. Однако может случиться, что в некоторой местности вторая разновидность будет лучше первой. Пусть некоторая интерпретация дисперсионного анализа была дана в предположении аддитивности. Если это предположение было принято только потому, что гипотеза отсутствия взаимодействий не была отвергнута некоторым F -критерием, то нужно посмотреть, имеет ли этот критерий разумную мощность отбрасывания гипотезы, если на самом деле взаимодействия достаточно велики, чтобы сделать неправильной интерполяцию, основанную на этой гипотезе.
Иногда случается, что гипотеза отсутствия взаимодействий отбрасывается статистическим критерием, а гипотеза нулевых главных эффектов обоих факторов принимается. В этом случае правильный вывод заключается в том, что не доказано отсутствие эффектов. Если есть ненулевые взаимодействия, то должны быть ненулевые разности средних ячейки. Заключение состоит в том, что разности есть, но когда эффекты уровней одного фактора усредняются по уровням другого, то доказывается отсутствие разности для этих усредненных эффектов.
Легко проверить, что свойство аддитивности эффектов сохраняется при линейных преобразованиях наблюдений и их средних  , но при нелинейных преобразованиях это свойство обычно нарушается. Представляет интерес решение следующей задачи: существует ли, если есть взаимодействие, подходящее преобразование шкалы измерений такое, что в новой шкале эффекты складываются. Эта практическая задача крайне сложна, так как нам неизвестны взаимодействия, и мы располагаем только оценками, которые имеют ошибку. В конце этого параграфа рассматривается более теоретическая задача преобразования в случае, когда взаимодействия известны. Все это представляет некоторый математический интерес и может обогатить наши представления о взаимодействиях.
, но при нелинейных преобразованиях это свойство обычно нарушается. Представляет интерес решение следующей задачи: существует ли, если есть взаимодействие, подходящее преобразование шкалы измерений такое, что в новой шкале эффекты складываются. Эта практическая задача крайне сложна, так как нам неизвестны взаимодействия, и мы располагаем только оценками, которые имеют ошибку. В конце этого параграфа рассматривается более теоретическая задача преобразования в случае, когда взаимодействия известны. Все это представляет некоторый математический интерес и может обогатить наши представления о взаимодействиях.
|
|
|


