Обоснование структуры регрессионной модели

 

Рассмотрим вариацию значений  относительно у. Справедливо разложение

где

-полная вариация , относительно среднего ;

-вариация относительно ,объясняемая регрессией;

-вариация регрессионных остатков.

 

.

Так как при этом число степеней свободы (число независимых слагае­мых в квадратичной форме)  равно сумме чисел степеней свободы сла­гаемых  и : , то, согласно теореме Кохрана, слагаемые  и  независимы между собой.

 

Разделив левую и правую часть выражения  на , получим:

 

Первое слагаемое в правой части полученного равенства есть оценка множественного коэффициента детерминации 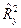, так как он характери­зует долю вариации у, обусловленную влиянием объясняющих перемен­ных  включенных в модель.

Тогда получим:

 .  Значение  свидетельствует о максимальной прогностической силе модели, когда по значениям  можно однозначно определить у, так как из условия следует, что для всех .

Когда , вариация остатков равна полной вариации у и отсутст­вует линейная зависимость между у и переменными .

Покажем, что в случае линейной зависимости между у и объясняю­щими переменными совпадают статистики критериев для про­верки нулевых гипотез H ₀:  и   H ₀: .

Преобразуем статистику для проверки гипоте­зы о значимости коэффициента детерминации (H ₀: )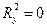

 

Мы получили в итоге статистику для проверки гипотезы о значимости уравнения регрессии (H ₀: ). Статистика  при вы­полнении гипотезы H ₀ имеет F -распределение с числами степеней свобо­ды числителя  и знаменателя .

Гипотезы H ₀ отвергается с вероятностью ошибки , если  будет больше критического значения , найденного по таблице F -распределения. Из этого следует, что 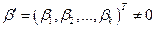, т. е. хотя бы один коэффициент регрессии не равен нулю.

В этом случае решается задача проверки значимости отдельных коэф­фициентов регрессии.

 

Доверительные интервалы коэффициентов  линейной регрессии

Пусть вектор ошибок ε имеет n -мерное нормальное распределение. В этом случае вектор Y наблюдений  также имеет нормальное распре­деление и из взаимной некоррелированности его элементов  следует их независимость. Оценка 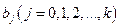имеет нормаль­ный закон распределения с математическим ожиданием  и дисперсией 

 , где .

Откуда  имеет нормированный, нормальный закон распределения.         

Статистика

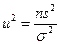
имеет распределение  с (п—k—1) степенями свободы.

Напомним, что случайная величина

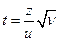
имеет распределение Стьюдента (t -распределение) с 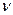  степенями свобо­ды, если z  имеет нормированное нормальное распределение , и  имеет распределение  с  степенями свободы , причем z и u не­зависимыми.

Получаем выборочную характеристику

,

 

которая имеет распределение Стьюдента с (п—k—1) степенями свободы.  Построим с надежностью   интервальную оценку для

.

Теперь определим интервальную оценку   в точке, определяемой век­тором   начальных условий, размерности (k+1):

.

Тогда несмещенная оценка с минимальной дисперсией значения при­знака  в точке, определяемой условиями , равна .

 В самом деле,

,

,

 

где — ковариационная матрица вектора оценок b.

Найдем доверительный интервал для :

,

которая имеет распределение Стьюдента с (п-k-1) степенями свободы. Из условия , раскрыв неравенство, стоящее в скобках, найдем интервальную оценку для  в точке, определяемой вектором  с надежно­стью :

,

где  определяется по таблице t -распределения Стьюдента для уровня зна­чимости 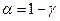 и числа степеней свободы (п-k-1).

Доверительная оценка для интервала предсказания  с надежно­стью  определяется как:

.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: