 |
Математическая модель распределительных задач
|
|
|
|
Специфика распределительных задач:
1) система ограничений представляет собой систему уравнений;
2) все коэффициенты при переменных системы ограничений равны единице;
3) каждая переменная в системе ограничений участвует только в двух соотношениях.
Система ограничений состоит из двух групп:
1) 
, 
;
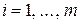2) 
, 
.
Выражение целевой функции:
.
Учитывая специфику распределительных задач, система ограничений дополняется условием
: 
.
Распределительная задача является задачей закрытого типа, если
,
в противном случае будем иметь задачу открытого типа. Существующий метод решения распределительной задачи применим только к задаче закрытого типа. Процедура приведения задачи открытого типа к закрытому типу связано с введением фиктивных участников.
Метод решения распределительной задачи называют методом потенциалов и характеристик. Потенциалы строк обозначают 
, для столбцов 
. Для расчета этих элементов используют формулу
,
для заполненных клеток таблицы расчетов распределительной задачи, где 
— элементы, называемые тарифами, присутствуют в таблицах расчетов распределительных задач и в целевой функции. Элемент, называемый характеристикой, обозначают 
. Она рассчитывается для свободных клеток таблицы расчетов распределительной задачи по формуле
.
Характеристика содержит важную информацию о качестве решения задачи (плана) — отражает величину экономии на единицу продукции за счет улучшения решения (плана) путем перераспределения продукции в свободную клетку таблицы. Таким образом, характеристика может являться критерием оптимальности решения задачи:
1) если задача решается на 
целевой функции, то критерием оптимального решения является отсутствие отрицательных характеристик в свободных клетках таблицы расчетов распределительной задачи;
|
|
|
2) если задача решается на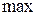 
целевой функции, то критерием оптимального решения является отсутствие положительных характеристик в свободных клетках таблицы расчетов распределительной задачи.
Процесс получения оптимального решения связан с улучшением неоптимального первоначального решения (пример первоначального решения приведен в таблице1). Затем производится расчет потенциалов строк и столбцов, а на их основании определяются характеристики свободных клеток. Анализируя характеристики на критерий оптимальности решения, строим контур перераспределения. Начало контура перераспределения находится в клетке с наименьшей отрицательной характеристикой, а движение продолжается либо по горизонтали, либо по вертикали таблицы до заполненной клетки, пока не вернемся в клетку, с которой было начато движение. Структура контура выбирается таким образом, чтобы можно было вернуться в первоначальную клетку. В клетках контура перераспределения проставляются чередующимися знаками 
и 
. Плюс начинается с первой клетки. Среди клеток со знаком выбираем клетку с минимальным значением. На эту величину и происходит перераспределение. В клетках со знаком 
все значения уменьшаются на величину перераспределения, а в клетках со знаком 
— увеличиваются. Улучшенное решение вновь проверяется на критерий оптимальности.
Таблица 3
Таблица для расчетов
|
|
| 1 | 2 | 3 |
|
| 
| 
| |||
| 1 |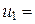 
| 
| 
| 
| 
|
| 2 | 
| 
| 
| 
| 
|
| 3 | 
| 
| 
| 
| 
|
| 4 |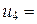 
| 
| 
| 
| 
|
| 
| 
| 
| 
|
Таблица 4
Пример одного из вариантов получения первоначального решения по методу северо-западного угла
|
|
| 1 | 2 | 3 |
|
|
|
|
| |||
| 1 |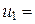
| 8000 | 8000 | ||
| 2 |
| 4000 | 1000 | 5000 | |
| 3 |
| 8000 | 2000 | 10000 | |
| 4 |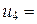
| 7000 | 7000 | ||
|
| 12000 | 9000 | 9000 | 30000=30000 |
|
|
|
Перед началом расчетов проверяем условие: количество заполненных клеток в первоначальном решении должно быть равно 
, где 
— количество строк, 
— количество столбцов таблицы. Если это условие не выполняется, значит, получаем один из случаев вырождения. Выход из такого положения будет пояснен ниже.
Случаи вырождения и их устранение:
1) при получении первоначального решения 
;
2) в контуре перераспределения встречаются клетки со знаком 
, имеющие одинаковые значения.
Варианты устранения случаев вырождения:
1) поменять местами столбцы таблицы, чтобы не выполнялось условие , либо построить первоначальное решение другим способом, чтобы не выполнялось условие ;
2) принять клетку с нулевым значением условно за занятую, т.е. ввести фиктивную занятую клетку.
Открытая модель распределительной задачи приводится к закрытой путем введения фиктивной строки или столбца, в зависимости от ситуации, чтобы модель стала закрытой. Фиктивная строка либо столбец должны иметь тарифы для хода расчетов в зависимости от характера задачи (min, max), чтобы исключить их в конечном итоге из решения задачи. Для широкого круга пользователей существует программа, с помощью которой производятся расчеты распределительных задач.
|
|
|
