Имитационное моделирование в задачах организации строительства

Появление имитационного моделирования и превращение его в эффективное средство анализа сложных систем было, с одной стороны, обусловлено потребностями практики, а с другой стороны, обеспечено развитием метода статистических испытаний (метод Монте-Карло), открывшего возможность моделирования случайных факторов, которыми изобилуют реальные системы, а также развитием электронной вычислительной техники, являющейся базой для проведения статистических экспериментов. Широкое применение метода имитации при управлении проектами  строительного комплекса обусловлено следующими причинами:

- сложность проектов, наличием большого числа факторов, которые ограничивают эффективность применения традиционных аналитических методов;

- новыми возможностями, которые позволяют осуществлять проведение имитационных экспериментов в широком диапазоне измерений параметров проекта и внешней среды, что позволяет получить полезную информацию в условиях информационной неопределенности;

- имитационное моделирование позволяет дать представление о том, какие из параметров проекта являются наиболее существенными.

При имитационном моделировании можно выделить следующие основные этапы:

- формулировка проблемы;

- построение математической модели;

- составление и отладка программ для ЭВМ, включая и разработку процедур моделирования различных случайных факторов;

- планирование экспериментов и обработка результатов исследования.

Как у любого метода исследования, у метода имитации есть и недостатки. В ряде случаев имитационные модели оказываются достаточно сложными, что требует больших временных и стоимостных затрат на их реализацию.

Анализ результатов имитации основан на использовании методов математической статистики. Для получения статистической достоверности результатов необходимо многократное повторение имитационных экспериментов, что требует временных затрат.

Однако, несмотря на отмеченные недостатки, метод имитационного моделирования широко используется при анализе сценариев проектов.

 

Метод статистического моделирования (Метод Монте-Карло)

Метод Монте-Карло состоит в реализации на компьютере ситуаций, определяемых случайными факторами с дальнейшей обработкой результатов экспериментов методами математической статистики.

Базой для имитации случайных ситуаций является так называемый «датчик случайных чисел».

Датчик случайных чисел – это реализованный на компьютере алгоритм формирования «псевдослучайных чисел», подчиненных равномерному на [0,1] распределении вероятностей. С помощью датчика случайных чисел можно смоделировать любое вероятностное распределение.

 

Пример 1

 

Для того, чтобы разыграть дискретную случайную величину Х, заданную законом распределения:

Х	х1	х2	…	хn
Р	р1	р2	…	рn

 

надо

1. Разбить интервал [0,1] на n интервалов:

D₁: [0, р₁],

D₂: [р₁, р₁ + р₂],

D₃: [р₁ + р₂, р₁ + р₂, р₃],

…

D_n: [р₁ + … + р_n-1, 1],

 

2. Выбрать из датчика случайных чисел случайное число r_j;

Если r_j попало в интервал D_i, то разыгрываемая случайная величина приняла возможное значение х_i

 

Пусть случайная величина Х имеет следующее распределение:

х	3	4	5	6
р	0,25	0,6	0,1	0,05

 

Тогда

D₁ = (0; 0,25)

D₂ = (0,25; 0,85)

D₃ = (0,85; 0,95)

D₄ = (0,95; 1)

 

Для получения пяти значений Х возьмем из датчика 5 чисел и применим к ним описанную выше процедуру.

rj	D i	х i
0,91	D4	6
0,46	D2	4
0,64	D2	4
0,03	D1	3
0,75	D2	4

Пример 2

Для того, чтобы разыграть возможное значение х _i непрерывной случайной величины X, зная ее распределение F(x), надо выбрать из датчика случайных чисел случайное число r_i, и найти х решением уравнения F(x)—r_i.

Пусть случайная величина X имеет экспоненциальное распределение с плотностью вероятностей:

,

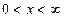
Тогда .  

Решением уравнения будет

.                                         (1)

Для получения 5 значений X возьмем из датчика случайных чисел 5 чисел и применим к ним формулу (1).

Пусть α = 2.

 

 

ri	X
0,46	0,39
0,20	0,8
0,28	0,63
0,40	0,46
0,85	0,08

 

Пример 3

Некоторые сложные распределения можно моделировать приближенно. Пусть X - нормальная случайная величина N (0,1). Для того, чтобы приближенно разыграть возможное значение х, надо сложить 12 случайных чисел из датчика случайных чисел и из полученной суммы вычесть 6:

.                                                   (2)

Если требуется разыграть нормальную случайную величину Y с математическим ожиданием   и дисперсией 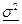, то соответствующая формула имеет вид:

.                                                    (3)

Пусть х: N (2; 3²)   (а = 2; = 3).

Взяв 12 чисел из датчика случайных чисел

0,37; 0,54; 0,2; 0,48; 0,05; 0,64; 0,85; 0,47; 0,42; 0,96; 0,24; 0,8;

получим из (2) х = 6,06 – 6 = 0,06.

Из (3) получаем у = 3 ^. 0,06 + 2 = 2,18.

Для моделирования можно воспользоваться датчиком случайных чисел из пакета Excel. Это мастер-функция СЛЧИС из списка математическим функций.

 

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: