Статистические гипотезы и правила их проверки. Статистические критерии.

Основные типы гипотез, проверяемых в ходе статистического анализа и моделирования

Гипотезы о типе закона распределения исследуемой случайной величины

Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей

Гипотезы о числовых значениях параметров исследуемой генеральной совокупности

Гипотезы об общем виде модели, описывающей статистическую зависимость между признаками

Понятие статистической гипотезы

Пусть 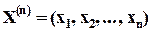- независимая повторная выборка объема 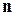из некоторой генеральной совокупности с неизвестной функцией распределения .

Под статистической гипотезой понимается всякое предположение о виде или параметрах неизвестного закона распределения.

Гипотеза есть определенное утверждение, которое по отношению к реальной ситуации является или истинным, или ложным высказыванием.

Простой статистической гипотезой называется предположение о соответствии неизвестной функции распределения некоторому конкретному распределению вероятностей.

Сложной статистической гипотезой называется предположение о том, что неизвестное распределение принадлежит некоторому множеству распределений, состоящему более чем из одного элемента.

Если удается выдвинуть две взаимоисключающие статистические гипотезы, содержащих в своей совокупности верное суждение о неизвестном распределении, то проверяемую гипотезу 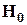принято называть основной (или нулевой), а противоположную гипотезу - альтернативой (или конкурирующей гипотезой).

Этапы проверки статистических гипотез

Формулировка основной гипотезы H₀ и конкурирующей гипотезы H₁. Гипотезы должны быть чётко формализованы в математических терминах.

Задание уровня значимости α, отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.

Расчёт статистики K критерия.

Построение критической области.

Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику K и по попаданию (или непопаданию) в критическую область W выносится решение об отвержении (или принятии) выдвинутой гипотезы H₀.

Статистический критерий

Правило, определяющее условия, при которых статистическая гипотеза отвергается или не отвергается [1], называется статистическим критерием.

Замечание. Статистический критерий не устанавливает, верна или нет выдвинутая гипотеза, а позволяет лишь проверить, противоречат или согласуются с гипотезой в рамках этого критерия выборочные данные.

Математическую основу критерия составляет выбираемая с учетом особенностей поставленной конкретной задачи специальная статистика , точное или приближенное распределение которой при выполнении гипотезы 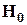известно.

В области возможных значений статистики критерия 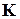выделяется множество , называемое критической областью (областью отвержения гипотезы).

 

При проверке гипотезы 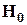руководствуются следующим правилом:

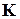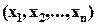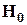если значение статистики критерия для выборки принадлежит критической области , то гипотеза отвергается, в противном случае - не отвергается.

В результате проверки гипотезы 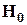при заданном критерии 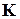; возможны верные решения двух следующих видов:

истинная гипотеза 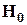не отвергается;

ложная гипотеза 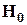отвергается.

Ошибка первого рода совершается, когда основная гипотеза 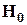верна, но отвергается в соответствии с заданным критерием .

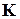Вероятность 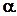ошибки первого рода называется уровнем значимости (или размером) критерия :

.

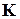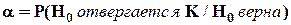На практике уровень значимости критерия задается изначально, исходя из потребностей реальных приложений и потенциальных последствий вероятных ошибок.

Ошибка второго рода допускается, когда альтернативная гипотеза верна, но отвергается в соответствии с заданным критерием 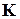(т.е. если основная гипотеза 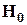не верна, но не отвергается).

Величина 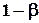, где 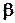- вероятность ошибки второго рода:

,

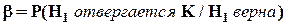называется мощностью критерия .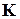

Замечание. Значение 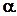(или 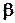) вычисляется по распределению вероятностей значений критической статистики в предположении, что неизвестное распределение генеральной совокупности отвечает гипотетически верному утверждению 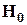(соответственно ):

; .

Вероятности ошибок первого и второго рода для любых гипотез и критериев находятся при разных предположениях о неизвестном распределении, что исключает наличие не зависящих от вида гипотез и критерия постоянных соотношений между ними.

Статистические критерии подразделяются на следующие категории:

Критерии согласия (Пирсона, Колмогорова-Смирнова) - проверка факта о том, что исследуемая случайная величина подчиняется предполагаемому закону. Критерии согласия можно также воспринимать, как критерии значимости.

Критерии однородности (Смирнова, Вилкоксона-Манна-Уитни, Стьюдента, критерий дисперсионного анализа, критерий однородности дисперсий, критерий Бартлетта) - случайные величины исследуются на факт взаимного соответствия их законов распределения (подчиняются ли эти величины одному и тому же закону).

Критерии проверки гипотез о числовых значениях параметров

содержание

 

⇐ Предыдущая25262728293031323334Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: