От Ксении (более полный ответ)

Компонентный и факторный анализы проводятся с несколькими целями. Как методы снижения размерности они позволяют выявить закономерности, которые непосредственно не наблюдаются. Эта задача решается по матрице нагрузок, как и классификация признаков в пространстве главных компонент (или общих факторов). А индивидуальные значения используются для классификации объектов (не по исходным признакам, а по главным компонентам или общим факторам) и для построения уравнения регрессии на эти обобщенные показатели.

Интерпретируются главные компоненты и общие факторы, которым соответствуют дисперсии больше 1, и которые имеют хотя бы одну весомую нагрузку. Выбор критической величины, при превышении которой элемент матрицы нагрузок признается весовым и оказывает влияние на интерпретацию главной компоненты или общего фактора, определяется по смыслу решаемой задачи и может варьировать в пределах от 0,5 до 0,9 в зависимости от получаемых промежуточных результатов. Формальные результаты должны хорошо интерпретироваться.

Факторный анализ - более мощный и сложный аппарат, чем метод главных компонент, поэтому он применяется в том случае, если результаты компонентного анализа не вполне устраивают. Но поскольку эти два метода решают одинаковые задачи, необходимо сравнить результаты компонентного и факторного анализов, т.е. матрицы нагрузок, а также уравнения регрессии на главные компоненты и общие факторы, прокомментировать сходство и различия результатов.

Компонентный анализ предназначен для преобразования системы k исходных признаков, в систему k новых показателей (главных компонент). Главные компоненты не коррелированны между собой и упорядочены по величине их дисперсий, причем, первая главная компонента, имеет наибольшую дисперсию, а последняя, k-я, наименьшую. При этом выявляются неявные, непосредственно не измеряемые, но объективно существующие закономерности, обусловленные действием как внутренних, так и внешних причин.

Компонентный анализ является одним из основных методов факторного анализа. В задачах снижения размерности и классификации обычно используются m первых компонент (m< k).

При наличии результативного показателя Y может быть построено уравнение регрессии на главных компонентах. На основании матрицы исходных данных:

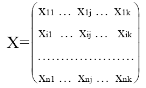
размерности (n×k), где x_ij – значение j-го показателя у i-го наблюдения (i=1,2,...,n; j=1,2,...,k) вычисляют средние значения показателей , а также s₁,..., s_k и матрицу нормированных значений:

с элементами:

Рассчитывается матрица парных коэффициентов корреляции:

с элементами: , где, j = 1,2,..., k.

 

На главной диагонали матрицы R, т.е. при j=l,

Модель компонентного анализа имеет вид:

(1), где:

a_iν – “вес”, факторная нагрузка, ν-ой главной компоненты на j-ой переменной;

f_iν – значение ν-й главной компоненты для i-го наблюдения (объекта),

где ν=1,2,...,k.

В матричной форме модель (1) имеет вид: ,

где: – матрица значений главных компонент размерности (n×k)

– матрица факторных нагрузок размерности (k×k).

А^Т – транспонированная матрица А;

f_iν – значение ν-й главной компоненты у i-го наблюдения (объекта);

a_jν – значение факторной нагрузки ν-й главной компоненты на j-й переменной.

 

Матрица F описывает n наблюдений в пространстве k главных компонент. При этом элементы матрицы F нормированы, то есть:

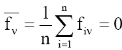, , а главные компоненты не коррелированны между собой. Из этого следует, что, (2),

 

где – единичная матрица размерности (k×k).

Выражение (2) может быть также представлено в виде:

(3) ν,ν ′ =1,2,..., k.

С целью интерпретации элементов матрицы А, рассмотрим выражение для парного коэффициента корреляции, между Z_j-переменной и, например, f₁-й главной компонентой. Так как, z_j и f₁ нормированы, будем иметь с учетом (1):

Принимая во внимание (3), окончательно получим:

Рассуждая аналогично, можно записать в общем виде:

для всех j=1,2,..., k и ν=1,2,..., k.

 

Таким образом, элемент a_jv матрицы факторных нагрузок А, характеризует тесноту линейной связи между z_j-исходной переменной и f_v-й главной компонентой, то есть

.

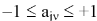Рассмотрим теперь выражение для дисперсии z_j-й нормированной переменной. С учетом (1) будем иметь:

, где ν, ν'=1,2,..., k.

 

Учитывая (3), окончательно получим:

(4)

По условию переменные z_j нормированы и s_j²=1. Таким образом, дисперсия z_j-й переменной согласно (4), представлена своими составляющими, определяющими долю вклада в нее всех k главных компонент.

Полный вклад ν-й главной компоненты в дисперсию всех k исходных признаков вычисляется по формуле:

Одно из основополагающих условий метода главных компонент, связано с представлением корреляционной матрицы R, через матрицу факторных нагрузок А:

 

Учитывая (2), окончательно получим:

 

Перейдем теперь непосредственно к отысканию собственных значений и собственных векторов корреляционной матрицы R.

Из линейной алгебры известно, что для любой симметрической матрицы R, всегда существует такая ортогональная матрица U, что выполняется условие: (5), где

– диагональная матрица собственных значений размерности (k*k)

– ортогональная матрица собственных векторов размерности (k*k)

 

Так как матрица R положительно определена, т.е. ее главные миноры положительны, то все собственные значения положительны – λ_ν>0 для всех ν=1,2,..., k.

В компонентном анализе элементы матрицы Λ ранжированы λ₁≥λ₂≥...≥λ_ν ≥...≥λ_k>0. Как будет показано ниже, собственное значение λ_ν характеризует вклад ν-й главной компоненты в суммарную дисперсию исходного признакового пространства.

Таким образом, первая главная компонента вносит наибольший вклад в суммарную дисперсию, а последняя k-я – наименьший.

В ортогональной матрице U собственных векторов, ν-й столбец является собственным вектором, соответствующим λ_ν-му значению.

Собственные значения λ₁≥...≥λ_ν≥...≥λ_k находятся как корни характеристического уравнения:

Собственный вектор V_ν, соответствующий собственному значению λ_ν корреляционной матрицы R, определяется как отличное от нуля решение уравнения, которое следует из:

Нормированный собственный вектор U_ν равен:

Из условия ортогональности матрицы U следует, что , но тогда по определению матрицы R и Λ подобны, так как они согласно (5) удовлетворяют условию:

Так как следы, т.е. суммы диагональных элементов у подобных матриц равны, то:

Напомним из линейной алгебры, что умножение матрицы U на обратную матрицу U^-1, дает единичную матрицу Е. Следы матричных произведений (U-1)×(RU) и R×(UU^-1) также равны.

Учитывая, что сумма диагональных элементов матрицы R равна k, будем иметь:

Таким образом, (6)

Представим матрицу факторных нагрузок А в виде: (7)

а ν-й столбец матрицы А: 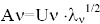, где U_ν – собственный вектор матрицы R, соответствующий собственному значению λ_ν.

Найдем норму вектора А_ν:

Здесь учитывалось, что вектор U_ν нормированный и . Таким образом,

Сравнив полученный результат с полным вкладом ν-й главной компоненты в дисперсию всех k исходных признаков (вычисляется по формуле ), можно сделать вывод, что собственное значение λ_ν характеризует вклад ν-й главной компоненты в суммарную дисперсию всех исходных признаков. Из (7) следует:

 

Согласно (6) общий вклад всех главных компонент в суммарную дисперсию равен k. Тогда удельный вклад ν-й главной компоненты определяется по формуле:

 

Суммарный вклад m первых главных компонент определяется из выражения:

Обычно для анализа используют m первых главных компонент, суммарный вклад которых превышает 60–70%.

Матрица факторных нагрузок А используется для экономической интерпретации главных компонент, которые представляют линейные функции исходных признаков. Для экономической интерпретации f_ν используются лишь те x_j, для которых, |а_jν|>0,5.

Значения главных компонент для каждого i-го объекта (i=1,2,...,n) задаются матрицей F.

Матрицу значений главных компонент можно получить из формулы: откуда, , где

Z – матрица нормированных значений исходных показателей.

 

Уравнение регрессии на главных компонентах строится по алгоритму пошагового регрессионного анализа, где в качестве аргументов используются главные компоненты, а не исходные показатели. К достоинству последней модели следует отнести тот факт, что главные компоненты не коррелированы. При построении уравнений регрессии следует учитывать все главные компоненты.

содержание

⇐ Предыдущая25262728293031323334Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: