 |
Гомо- и гетероскедастичность остатков в регрессионных моделях.
|
|
|
|
Термин гетероскедастичность в широком смысле означает предположение о дисперсии случайных ошибок регрессионной модели. Случайная ошибка – отклонение в модели линейной множественной регрессии: 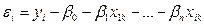
Величина случайной регрессионной ошибки является неизвестной, поэтому вычисляется выборочная оценка случайной ошибки регрессионной модели по формуле: 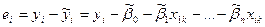 , где
, где  - остатки регрессионной модели.
- остатки регрессионной модели.
Нормальная линейная регрессионная модель строится на основании следующих предположения о случайной ошибке:
Матожидание случайной ошибки уравнения регрессии равно 0 во всех наблюдениях:  , где
, где 
Дисперсия случайной ошибки уравнения регрессии является постоянной для всех наблюдений: 
Случайные ошибки уравнения регрессии не коррелированны между собой, то есть ковариация случайных ошибок любых двух разных наблюдений равна 0: 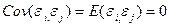 , где
, где 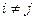
Условие  трактуется как гомоскедастичность (однородный разброс) дисперсий случайных ошибок регрессионной модели. Гомоскедастичность – это предположение от том, что дисперсии случайной ошибки
трактуется как гомоскедастичность (однородный разброс) дисперсий случайных ошибок регрессионной модели. Гомоскедастичность – это предположение от том, что дисперсии случайной ошибки 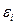 является известной постоянной величиной для всех
является известной постоянной величиной для всех 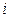 наблюдений регрессионной модели. На практике предположение о гомоскедатичности случайной ошибки
наблюдений регрессионной модели. На практике предположение о гомоскедатичности случайной ошибки 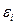 или остатков регрессионной модели
или остатков регрессионной модели  далеко не всегда оказывается верным. Предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, называется гетероскедастичностью (неоднородный разброс).
далеко не всегда оказывается верным. Предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, называется гетероскедастичностью (неоднородный разброс).  , где
, где 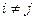 .
.
Условие гетероскедастичности можно записать через ковариационную матрицу случайных ошибок регрессионной модели.
 , где
, где 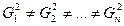
Тогда 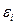 подчиняется нормальному закону распределения с параметрами:
подчиняется нормальному закону распределения с параметрами: 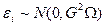 , где
, где 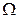 - матрица ковариации случайной ошибки.
- матрица ковариации случайной ошибки.
|
|
|
Если дисперсии случайных ошибок регрессионной модели 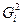 известны заранее, то от проблемы гетероскедастичности можно было бы легко избавиться. Но на практике, как правило, неизвестна даже точная функция зависимости
известны заранее, то от проблемы гетероскедастичности можно было бы легко избавиться. Но на практике, как правило, неизвестна даже точная функция зависимости 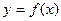 между изучаемыми переменными, которую предстоит построить и оценить. Чтобы в подобранной регрессионной модели обнаружить гетероскедастичность, необходимо провести анализ остатков регрессионной модели. Проверяются следующие гипотезы:
между изучаемыми переменными, которую предстоит построить и оценить. Чтобы в подобранной регрессионной модели обнаружить гетероскедастичность, необходимо провести анализ остатков регрессионной модели. Проверяются следующие гипотезы:
Основная гипотеза  , утверждающая о постоянстве дисперсий случайных ошибок регрессии, то есть о присутствии в модели условия гомоскедастичности:
, утверждающая о постоянстве дисперсий случайных ошибок регрессии, то есть о присутствии в модели условия гомоскедастичности: 
Альтернативной гипотезой 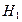 является предположение о неодинаковых дисперсиях случайных ошибок в различных наблюдениях, то есть о присутствии в модели условия гетероскедастичности:
является предположение о неодинаковых дисперсиях случайных ошибок в различных наблюдениях, то есть о присутствии в модели условия гетероскедастичности: 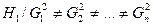
Обнаружение гетероскедастичности.
Существует несколько тестов на обнаружение гетероскедастичности в регрессионной модели.
Тест Глейзера.
На первом этапе строится обычная регрессионная модель: 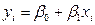
Методом наименьших квадратов вычисляются оценки коэффициентов построенной модели: 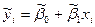
На следующем этапе вычисляются остатки регрессионной модели: 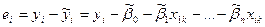 .
.
Полученные регрессионные остатки возводятся в квадрат 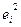 .
.
С целью обнаружение гетероскедастичности определяется коэффициент Спирмена.
Коэффициент Спирмена является аналогом парного коэффициента корреляции, но позволяет выявить взаимосвязь между качественным и количественным признаками. Зависимой переменной является 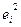 , в качестве независимой выступает
, в качестве независимой выступает 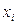 . Переменная
. Переменная 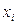 ранжируется и располагается оп возрастанию. Ранги обозначаются как
ранжируется и располагается оп возрастанию. Ранги обозначаются как  . Далее проставляются ранги переменной
. Далее проставляются ранги переменной 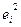 , обозначаемые как
, обозначаемые как 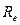 .
.
Коэффициент Спирмена рассчитывается по формуле: 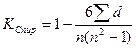 , где d – ранговая разность (
, где d – ранговая разность ( -
- 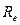 ); n – количество пар вариантов.
); n – количество пар вариантов.
Значимость коэффициента Сирмена проверяется с помощью t-критерия Стьюдента.
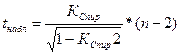
Критическое значение определяется по таблице распределения Стьюдента:  .
.
|
|
|
Если  , то основная гипотеза отвергается, и между переменной
, то основная гипотеза отвергается, и между переменной 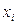 и остатками регрессионной модели
и остатками регрессионной модели  существует взаимосвязь, то есть в модели присутствует гетероскедастичность.
существует взаимосвязь, то есть в модели присутствует гетероскедастичность.
Если 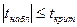 , то основная гипотеза принимается, и в модели парной регрессии гетероскедастичность отсутсвует. Для модели множественной регрессии вывод может быть следующий: гетероскедастичность не зависит от выбранной переменной
, то основная гипотеза принимается, и в модели парной регрессии гетероскедастичность отсутсвует. Для модели множественной регрессии вывод может быть следующий: гетероскедастичность не зависит от выбранной переменной 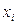 .
.
Устранение гетероскедастичности.
Наиболее простым методом устранение гетероскедастичности является взвешивание параметров регрессионной модели. Суть метода состоит в том, что отдельным наблюдениям независимой переменной с максимальным среднеквадратическим отклонением случайной ошибки придается больший вес, а остальным наблюдениям с минимальным среднеквадратическим отклонением случайной ошибки придается меньший вес. Благодаря этому оценки коэффициентов уравнения остаются эффективными. Модель регрессии при таком подходе называется взвешенной регрессией с весами 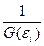 .
.
Рассмотрим процесс взвешивания для линейной модели парной регрессии, в которой доказано наличие гетероскедастичности:  , где
, где 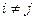 .
.
Разделим регрессионное уравнение на среднеквадратическое отклонение случайной ошибки 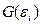 :
:
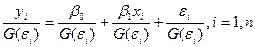
Данное уравнение записывают в линейном виде с помощью метода замен. Введем обозначения: 
Уравнение регрессии записывают в преобразованном виде: 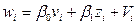
Эта регрессионная модель является моделью с двумя факторными переменными  и
и 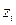 .
.
Дисперсия случайной ошибки взвешенной регрессионной модели: 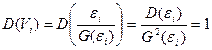
Основной проблемой рассмотренного подхода к устранению гетероскедастичности является необходимость априорного знания среднеквадратических отклонений случайных ошибок регрессионной модели. Такое условие в реальности практически невыполнимо, приходится прибегать к другим методам устранения гетероскедастичности.
Методы коррекции гетероскедастичности сводятся к нахождению ковариационной матрицы случайных ошибок регрессионной модели.
 , где
, где 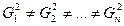
Оценки 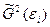 находятся с помощью метода Бреуше-Пайана:
находятся с помощью метода Бреуше-Пайана:
На основании уравнения регрессии находятся остатки  и сумма квадратов остатков
и сумма квадратов остатков 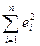
Оценкой дисперсии остатков регрессионной модели будет величина: 
|
|
|
Строится взвешенная регрессия, где весами является оценка дисперсии остатков регрессионной модели 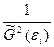
Если взвешенное уравнение получается незначимым, то и оценки матрицы ковариаций 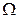 являются неточными.
являются неточными.
После нахождения оценок дисперсий остатков можно воспользоваться доступным обобщенным или взвешенным методом наименьших квадратов для вычисления оценок коэффициентов уравнения регрессии, которые различаются лишь оценкой 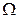 . Если нельзя выполнить коррекцию гетероскедастичности, то вполне возможно вычислить оценки коэффициентов уравнения регрессии по обычному МНК, но корректировать ковариационную матрицу оценок коэффициентов
. Если нельзя выполнить коррекцию гетероскедастичности, то вполне возможно вычислить оценки коэффициентов уравнения регрессии по обычному МНК, но корректировать ковариационную матрицу оценок коэффициентов 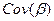 , так как условие гетероскедастичности приводит к увеличению данной матрицы.
, так как условие гетероскедастичности приводит к увеличению данной матрицы.
содержание
|
|
|


