 |
A2.1. Дискретное управление модой в многомодовом волокне
|
|
|
|
Многомодовое волокно состоит из цилиндрического ядра с коэффициентом преломления n 1 и радиусом a и окружающей оболочки с более низким показателем преломления n 2< n 1 (Рисунок A2.1). Из-за граничных условий на поверхности ядро-оболочка существует ряд дискретных собственных решений общего уравнения переноса, которые направлены в
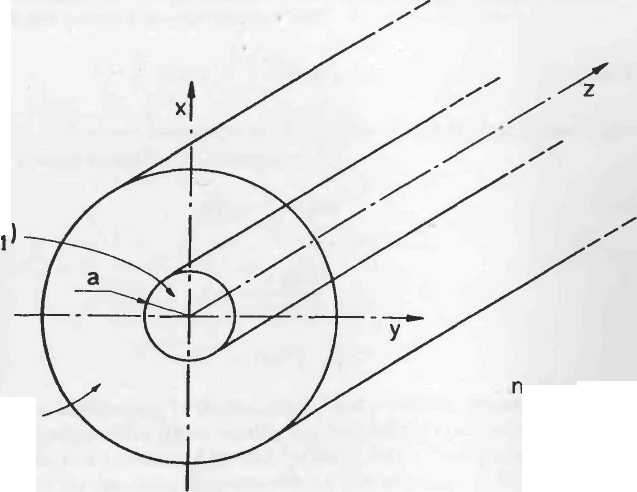
| Рисунок А2.1. Оптическое волокно |
| Ядро (n 1) |
| Оболочка (n 2) |
| n 1> n 2 |
волокно. Эти собственные решения называются модами волокна, которое считается многомодовым. Они могут быть написаны:
(A2.1)
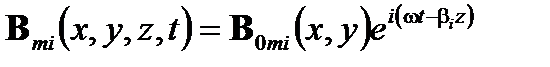
где x и у – поперечные пространственные координаты, а z является продольной пространственной координатой, соответствующей направлению распространения.
В противоположность случаю плоской волны каждая мода имеет специфическое поперечное распределение поля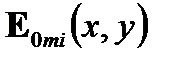 
и 
, которые стремятся к нулю при удалении от ядра. Перенос фазового члена 
зависит от угловой частоты ω и для конкретных мод распространения постоянная β i, которая зависит от ω и находится между значениями волнового числа k 2 в оболочке и волнового числа k 1 в ядре:
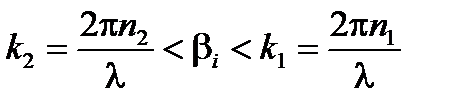(A2.2)
Для i -й моды часто используют эквивалентный показатель преломления 
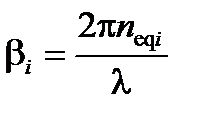
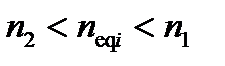(A2.3)
Моды электромагнитного поля обозначаются ТЕ для поперечной электрической или ТМ для поперечной магнитной, или EH и НЕ для гибридной электромагнитной, поскольку они имеют продольные компоненты Еz или Bz в дополнение к обычным поперечным компонентам (Ex, Ey) и (Bx, By) к ТЕ волнам на свободной поверхности: ТЕ моды имеют продольные магнитные компоненты, ТМ моды имеют продольные электрические компоненты, а EH и НЕ моды имеют продольные компоненты для обоих полей E и В.
На практике разность показателей преломления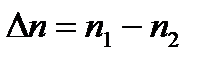 
мала: относительная разность показателей преломления 
обычно порядка 0,2% до 1%. Это дает незначительные продольные компоненты и моды, затем, обозначая LP линейную поляризацию, можно рассматривать их как обычные поперечные волны.
|
|
|
Основным интересом этого модального разложения является тот факт, что набор мод является ортонормальным базисом собственного ансамбля векторов всех возможных решений уравнения распространения. Этот ансамбль с математической точки зрения является линейным пространством скалярных произведений.
Наиболее знакомым линейным пространством является геометрическое трехмерное пространство. Любой вектор U может быть разложен на ортонормальный базис собственных векторов (a1, a2, a3):
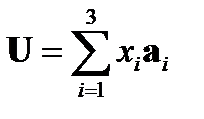(A2.4)
Ортонормальный базис является ортогональным; то есть, скалярное произведение двух различных собственных векторов равно нулю:
и это также нормально; то есть все квадраты скаляров собственных векторов равны:
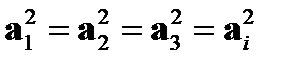
Норма или амплитуда или модуль U вектора U определяется как квадратный корень из ее скалярного квадрата
Есть два важных результата, которые могут выглядеть очевидными, или по крайней мере, очень фамильярными в геометрическом пространстве, но которые являются чрезвычайно полезными в других линейных пространствах, для которых это не так просто:
• Координата x является
(A2.5)
• Квадрат модуля является
(A2.6)
В частности, очень удобно считать, что ансамбль комплексных функций f (x), которые показывают площади как интегралы в линейном пространстве. Бесконечный интеграл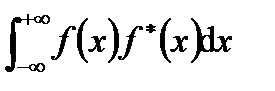 
является сходящимся (который определяет площадь подинтегральной функции) и может рассматриваться как площадь обобщенного скаляра 
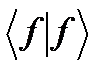функции. Обобщенное скалярное произведение может быть определено как
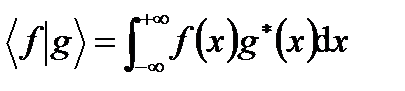(A2.7)
Это можно найти на ортонормированном базисе собственных функций (fi) этого линейного пространства, какой-либо функции f, соответственно разлагаемой на:
|
|
|
(A2.8)
с 
и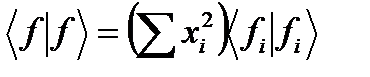 
Тот факт, что линейное пространство функций f имеет бесконечное измерение, не приводит к изменению общего характера приведенных выше результатов, и это определение скалярного произведения может быть применено до функции нескольких переменных с несколькими интегралами.
Возвращаясь к волокну, ансамбль решений уравнения распространения является также линейным пространством, которое является суммой несветоводных решений и суммой световодных решений. Размерность ансамбля несветоводных решений бесконечна, но конечна размерность ансамбля световодных решений: она равна числу мод в волокне. Любое решение E уравнения распространение может быть разложено:
(A2.9)
где e mi – нормализованные направляемые моды и e ri – ненаправляемые моды, которые излучают.
Направляемые моды e mi (x, y, z, t) являются собственными векторами, и, следовательно, их обобщенные скалярные произведения 
нули. Устраняя z и t зависимости, эти обобщенные скалярные произведения дают для распределений поперечного поля так называемые частично перекрывающиеся интегралы, которые также равны нулю для ортогональных мод:
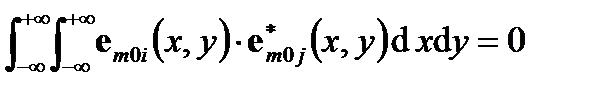(A2.10)
Координаты xi мод е mi поля E определяется обобщенным скалярным произведением:
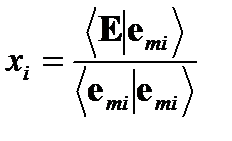(A2.11)
аналогичные определения координат вектора в геометрии с
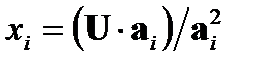(A2.12)
С частично перекрывающимися интегралами устранена зависимость (z, t):
(A2.13)
Кроме того аналогично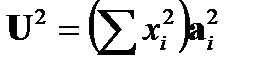 
в геометрии, существует также:
(A2.14)
С точки зрения физики это последнее уравнение показывает, что суммарная мощность волны E должно равняться сумме мощностей всех мод, как мы могли бы ожидать. Фактически квадрат электрического поля пропорционален интенсивности волны (т.е. пространственной плотности мощности) и бесконечный интеграл частичного перекрытия дает суммарную мощность, являющуюся плотностью мощности в поперечной плоскости xy.
Это отношение применяется только к общей мощности мод. Проблема заключается в очень разных локальных плотностях мощности в ядре. Квадраты суммарных амплитуд этих мод и являются результатом интерференции между различными модами. В частности, имеются места без света в связи с деструктивной интерференцией. С большим количеством мод это дает пятнистый узор.
|
|
|
Заметим, что частично перекрывающиеся интегралы с использованием «обычного» скалярного произведения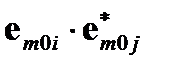 
действительны с предположением поперечных LP мод, когда разность коэффициентов преломления невелика. Как правило, где есть продольное поле компонентов, выражение 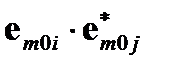должно быть заменено векторным произведением 
. Это делает вычисления более сложными, но основной принцип ортогональности мод сохраняется.
A 2.2. Одномодовые волокна
Расчет мод обычно осуществляется с нормализованной частотой V вместо угловой частоты ω. Это определяется с:
(A2.15)
Это может быть написано:
(A2.16)
где 
– числовая апертура волокна, как определено в Приложении 1. Существует также:
(A2.17)
Важным результатом является то, чтопри 
шаговый коэффициент волокна в одномодовом режиме, при котором можно руководствоваться только основными пространственными модами (символы НЕ11 или LP01). Значение 2,405 есть первая нулевая функция Бесселя J 0. Отсекаемая длина волны λ с определяется как:
(A2.18)
то есть 
и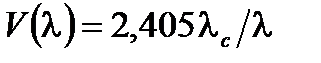 
Волокно является одномодовым для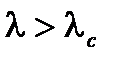 
. Отметим, что идеальное одномодовое волокно может пропускать любое состояние поляризации с одним и тем же постоянным распространением: двухмерные линейные пространственные поляризационные моды, как говорят, выродились.
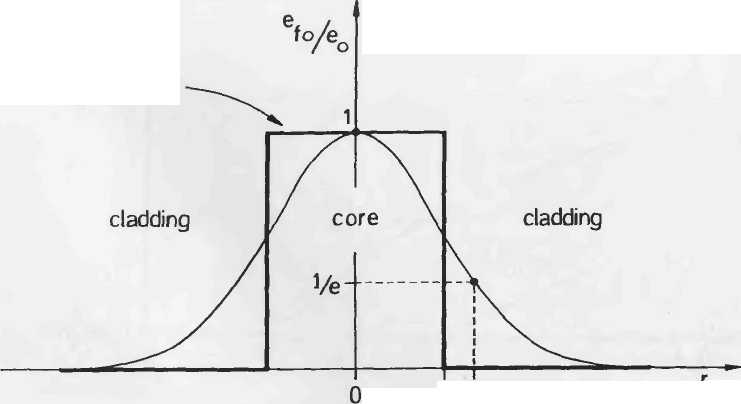
Точное определение мод требует использования Бесселя и модифицированных Бесселевых функций, но основные моды можно аппроксимировать распределением по Гауссу, для амплитуд волн получим, (Рисунок A2.2):
| Оболочка |
| Ядро |
| Оболочка |
| (Амплитуда)а |
| Ступенчатый профиль |
| a w0 r |
| Рисунок A2.2. Псевдогауссова амплитуда основной LP01 моды одномодового волокна (случай, когда λ=1,2λс) |
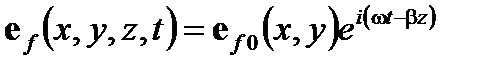
(A2.19)
где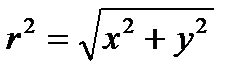 
– радиальная координата. Радиус моды w 0 (как 1/ e в амплитуде и 1/ e 2 в интенсивности) для 
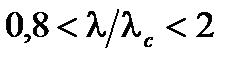(Рисунок А.2.3)
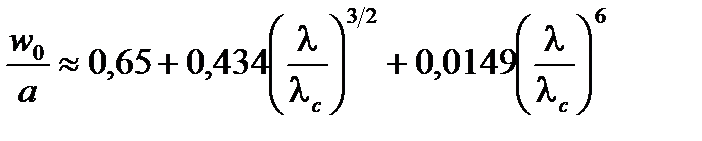(A2.20)
Даже простое линейное приближение является обычно достаточно точным в пределах практического использования одномодового волокна (т.е., 1< λ/λ c <1,5):
|
|
|
(A2.21)
| Линейный интервал |
| Одна мода |
| Рисунок A2.3. Основные LP01 моды радиуса w 0 в зависимости от длины волны λ |
Постоянная распространения β варьируется от k 2 для бесконечно длинных волн до k 1 для волн нулевой длины:
• При очень больших длинах волн моды весьма широкие и "наблюдаются" главным образом в оболочке с ее показателем преломления n 2,
• При очень коротких длинах волн моды ограничиваются в ядре и "наблюдаются" главным образом в ядре с его показателем преломления n 1.
Постоянная нормализованного распространения b (V) часто используется с
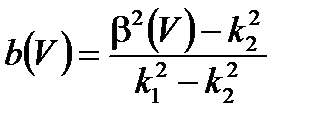
(A2.22)
В случае небольших разностей относительного показателя преломления мы можем написать:
или 
(A2.23)
Для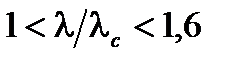 
, когда значение 
может быть аппроксимировано путем (Рисунок A2.4):
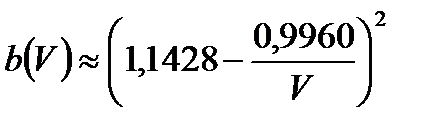
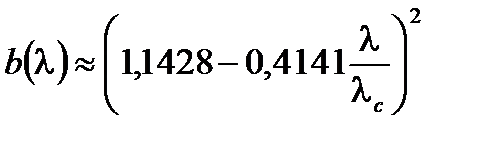(A2.24)
| Одна мода |
| n 1 или 1 |
| n 2 или 0 |
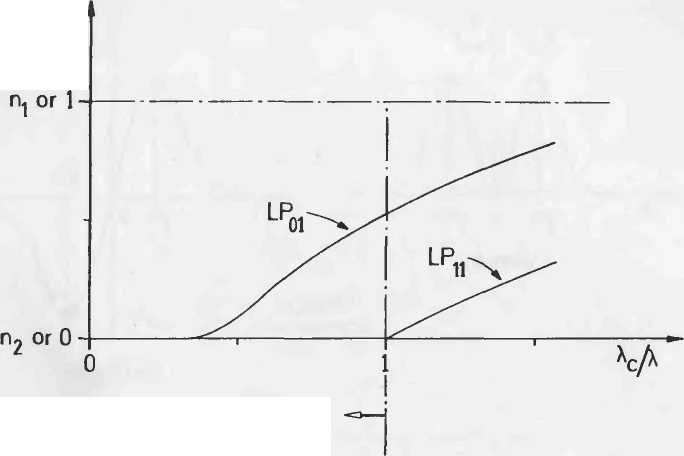
| n eq или b (λ) |
| Рисунок А.2.4. Постоянная распространения b (λ) и эквивалентный индекс n eq при LP01 и LP11 модах |
Затем на пределе одномодового режима
(A2.25)
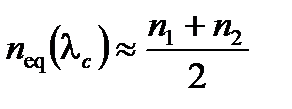(A2.26)
Обратите внимание, что зависимость длины волны от постоянной распространения b (λ) дает эффекты дисперсии благодаря направленному распространению в дополнение к собственной хроматической дисперсии материала. В частности модулированные сигналы распространяются с групповой скоростью:
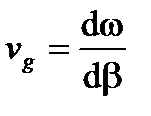(A2.27)
(A2.28)
с
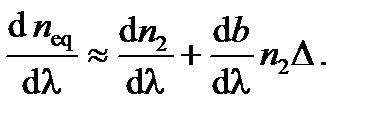(A2.29)
Этот анализ был получен для волокна с совершенным ступенчатым профилем; тем не менее, с некоторых конкретных производственных процессов появилось некотороее постепенное изменение ступенчатого профиля. Оценка характеристик таких волокон, как правило, проводится с использованием волокон с эквивалентным ступенчатому профилем, который обеспечивает просто приближенные значения отсечки и диаметра моды. В частности, коэффициент параболического профиля максимального радиуса a max и максимальной относительной разности показателей преломления Δmax может быть аппроксимирована с эквивалентным ступенчатому профилем радиусом ae = 0,8 a max и относительной разностью показателей преломления Δ е =0,75Δmax (Рисунок А 2.5).
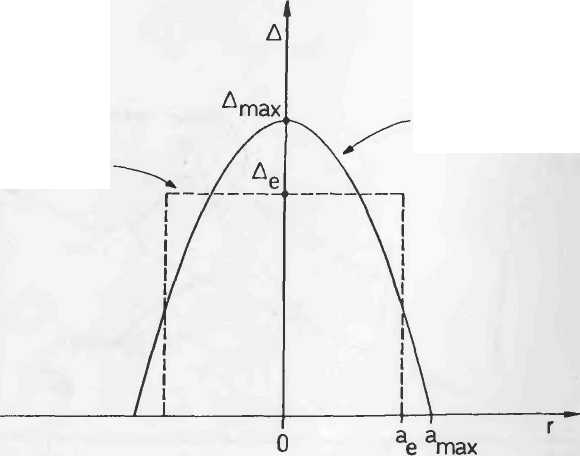
| Параболический профиль |
| Эквивалентный ступенчатый профиль |
| Рисунок А2.5. Эквивалентная ступень параболического профиля |
Теперь, когда волокно используется ниже его одномодовой отсечки, существуют моды более высокого порядка распространения. В частности, когда 0,63λ с <λ<λ c (т.е., 2,4< V <3,8) антисимметричная LP11 мода становится направляемой в дополнение к основной LP01 моде. Эта мода второго порядка имеет нечетное распределение применительно к одной поперечной координате. Амплитуда волны может быть приблизительно описана с помощью нормализованных производных гауссовской функции (Рисунок A2.6):
|
|
|
| Амплитуда |
| Возведение в квадрат |
| Интенсивность |
| Рисунок A2.6. Амплитуда и интенсивности распределения моды LP11 второго порядка |
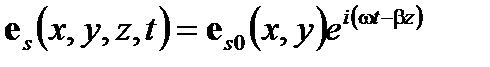
(A2.30)
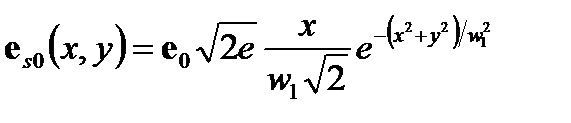
Эта мода состоит из двух доль, амплитуда (или поле) которых имеет противоположные знаки (или различие по фазе на π рад). С другой стороны, интенсивность (или мощность), которая зависит от квадрата амплитуды (или поля), является идентичной и всегда положительно влияет на обе доли. Поле e s 0 максимально и равнo e 0 для x = w 1 и у =0. Значение w 1 является максимально полуширинными.
Мода LP11 является вырожденной с точки зрения поляризации в качестве LP01 моды, но она также имеет пространственную вырожденность, поскольку доли может быть выровнены по любой поперечной оси (Рисунок A2.7).
|
|
|
