A4.1. Специальная теория относительности и электромагнетизм

Специальная теория относительности базируется на принципе эквивалентности так называемой инерциальной системы отсчета для всех законов физики, особенно механики и электромагнетизма: главный эффект состоит в том, что скорость света в вакууме та же, что и в любой инерциальной системе.

Это дает преобразования Лоренца между пространственными координатами и временем для двух систем, движущихся с постоянной скоростью переноса v_t, (вдоль оси x) относительно друг друга:

 

(A4.1)

с

По сравнению с классической механики преобразования Галилея:

(A4.2)

 

Есть разница второго порядка (в v_t / c) для пространственной координаты x и разница первого порядка по времени t.

«Упрощенные» и сжатые уравнения законов относительности обычно выражают в четырехмерной записи, используя контравариантные и ковариантные координаты 4 векторов и тензоры. Пространственно-временное четырехвекторное ⁴ x имеет контравариантные координаты, определяемые

 

(A4.3)

 

и ковариантные координаты, определяемые

 

(A4.4)

 

Контравариантные координаты это «обычные» координаты

 

(A4.5)

 

где – собственные базисные векторы. В четырехмерном пространстве член пропущен, и условно суммирование проводится по любым двойным индексам, появляющимся раз вверх и один раз вниз.

 

(A4.6)

 

Ковариантные координаты определяются скалярным произведением:

 

(A4.7)

 

В ортонормальном базисе евклидовой системы отсчета контравариантные и ковариантные координаты равны. Некоторая ощущаемая разницу между контравариантными и ковариантными координатами может быть получена в неортогональной двумерной плоскости (Рисунок А 4.1). Контравариантные координаты являются обычными координатами, определяемые параллелограммом с длинами сторон, равными x ¹ и x ². Ковариантные координаты определяются скалярными произведениями x·а₁ и x·а₂ соответственно перпендикулярно проекциям x на каждой координатной оси.

Ковариантные координаты связаны с "обычными" контравариантными координатами ковариантным тензором второго порядка, так называемым

 

Рисунок А4.1. Геометрическое представление контравариантных координат xµ и ковариантных координат xµв двумерной плоскости

метрическим тензором 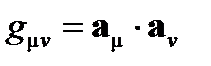, который характеризует систему отсчета:

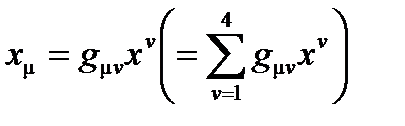(A4.8)

 

В инерциальной системе отсчета имеем

 

(A4.9)

 

Теперь преобразования Лоренца могут быть написаны с

 

где

(A4.10)

 

Обратите внимание, что 4-векторная «длина» и ее квадрат, определяемые скалярным произведением, это инвариантные преобразования Лоренца

 

(A4.11)

или

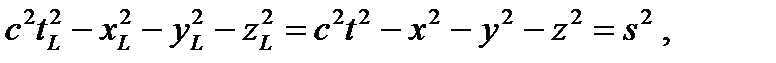(A4.12)

 

где s ² – так называемый пространственно-временной инвариант.

Электромагнетизм также может быть описан этим четырехмерным формализмом. Потенциальный вектор А и скалярный потенциал V образуют четырехвектор ⁴ А с контравариантными компонентами:

 

(A4.13)

 

и ковариантные компоненты:

 

(A4.14)

 

Этот четырехпотенциал определяет электромагнитное поле, представленное ковариантным антисимметричным тензором второго ранга . С обычными определениями и , могут быть записаны

(A4.15)

 

где 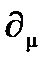– ковариант и соответствует частной производной применительно к пространственно-временным контравариантным координатам 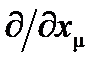. Из этого определения можно увидеть, что является антисимметричной, поскольку . Выражая компоненты полей E и В, ковариантные компоненты полей являются тензором

 

(A4.16)

 

где μ – столбцы коэффициентов и v – строки коэффициентов. Контравариантные компоненты представлены

 

(A4.17)

 

где 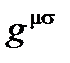– контравариантный метрический тензор, связанный с ковариантным метрическим тензором :

 

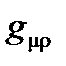(A4.18)

У нас есть

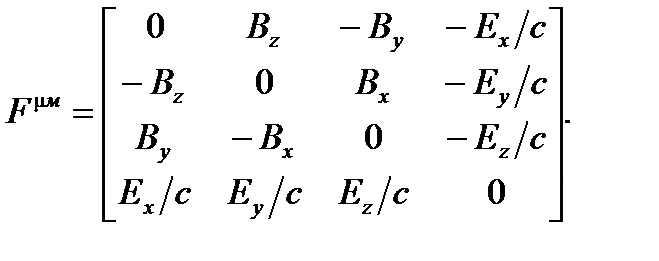(A4.19)

 

Первые два уравнения Максвелла M₁ и M₂ выражают тот факт, что поля является производными от потенциал и могут быть записаны

 

(A4.20)

 

Также можно определить четырехтоковый вектор ⁴ J с

 

(A4.21)

Последние два уравнения Максвелла, М₃ и M₄ могут быть записаны как

 

(A4.22)

 

Обратите внимание, что первые два уравнения Максвелла используют ковариантные координаты и два последние уравнения используют контравариантные координаты .

Наконец, уравнение распространения

 

(A4.23)

 

где и , то есть:

 

(А4.24)

 

Важно отметить, что уравнения Максвелла и их последствия, как уравнение распространения, инвариантны при преобразовании Лоренца. В новом 4- векторном и тензорном 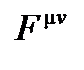преобразовании соответственно

(A4.25)

 

и эти величины следуют тем же законам. В частности уравнение распространения

(A4.26)

 

с и . Этот результат согласуется с тем фактом, что скорость света в вакууме остается равной с в любой инерциальной системе отсчета.

Обратите внимание, что уравнение лежит в основе магнетизм. С неподвижными зарядами есть только электрическое поле E и три остальные магнитные компоненты из равны нулю:

 

 

Учитывая эффект движущихся зарядов, мы должны использовать преобразование Лоренца в подвижной системе координат, где заряды движутся с противоположными скоростями – v_t, если v_t является скоростью перемещения системы отсчета с неподвижными остальными частицами. Рассчитывая , мы получаем ненулевые условия для , то есть отображения магнитных компонент В: даже если они иногда устраняются, магнитное поле это чисто релятивистский эффект. Поскольку скорость частиц обычно намного меньше, чем c, чистый эффект В обычно намного меньше, чем Е. Тем не менее, если это относится к одной частице, в случае проводника, то есть аннулирования E эффекта, в котором имеется много как положительных частиц, так и отрицательных, хотя эффект В не отменяется, поскольку положительные и отрицательные частиц не имеют одинаковую скорость. В этом случае глобальный В эффект становится преобладающим, несмотря на тот факт, что элементарный В эффект для каждой частица является более низким эффектом. Как будет видно, проблема эффекта Саньяка имеет некоторое сходство с этим магнитным полем: это эффект также первого порядка, который гораздо меньше, чем эффект нулевого порядка; но эффект нулевого порядка может также быть обнуляющим из-за взаимности и в кольцевом интерферометре эффект первого порядка может стать преобладающим.

Основным интересом этих рассуждений является то, что эти результаты остаются почти неизменными в любой системе координат, даже если они не являются декартовыми. В целом мы по-прежнему имеем

 

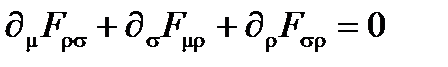
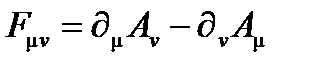(A4.27)

 

и два последних уравнения Максвелла слегка изменяются:

 

(A4.28)

 

где g является определяющим метрическим тензором. В инерциальной системе отсчета и декартовых координатах имеем и .

В случае уравнения распространения это намного сложнее, поскольку оно использует производные "высокого порядка" в дополнение к производным "низкого порядка" 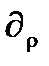, который используются в других формулах, и нет простого обобщения уравнения. Чтобы избежать этих математических трудностей, можно определить уравнение распространения четырехпотенциалом . Фактически, уравнения

(A4.29)

 

дают уравнение распространения:

 

(A4.30)

 

К настоящему времени этот анализ был проведен с предположением, что существует вакуум. Если есть среда, должно быть использовано тензорное поле производных с компонентами D и H. Первые два уравнения Максвелла, которые показывают связь с потенциалом, остались прежними, но два последних из них становятся

(A4.31)

где – свободный 4-векторный ток.

Тензорное поле производных связано с тензорным полем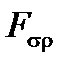

 

(A4.32)

 

где – составляющие тензора материала. Это зависит от относительной диэлектрической проницаемости ε _r и относительной магнитной проницаемости μ _r, но и от метрической системы отсчета, начиная с , использующей конровариантные координаты и , использующей ковариантные координаты.

В инерциальной системе отсчета имеем

 

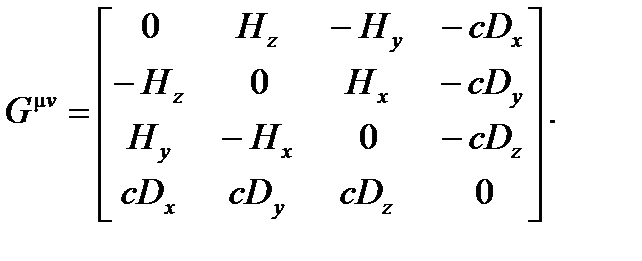(A4.33)

 

И ненулевые члены составляющего тензора 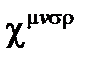неподвижного материала

 

(A4.34)

 

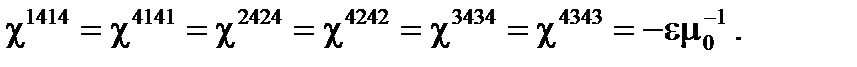(A4.35)

 

В общем случае уравнение распространения является четырехпотенциалом

 

(А4.36)

 

В качестве примера этого анализа мы можем рассмотреть случай цилиндрических координат с контравариантными (т.е., «обычными») значениями:

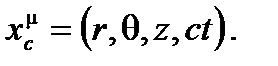(A4.37)

Метрический тензор это:

(A4.38)

 

Таким образом, детерминанта g_c=–r ²и и ковариантные координаты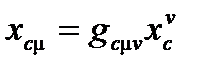

(A4.39)

 

Электромагнитный четырехпотенциал ⁴А _с определяется контравариантными координатами:

 

(A4.40)

 

где А_r, А _θ и А_z являются обычными координатами A с ортогональными единичными векторами a _r, а_θ и a _z, параллельными соответствующим координатным линиям (Рисунок А 4.2). Ковариантные координаты

 

(A4.41)

 

Рисунок А 4.2. Цилиндрические координаты

Для ковариантных компонентов имеется аналогичное тензорное поле

 

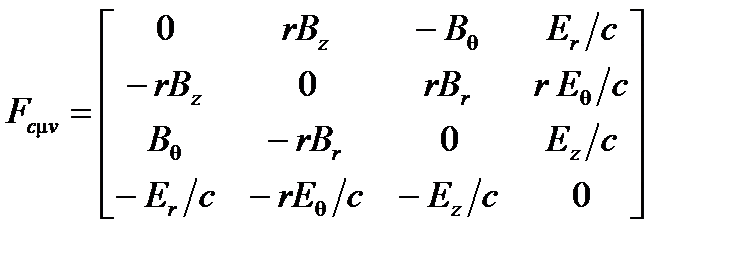(A4.42)

 

и для контравариантных компонентов получаем тензорное поле

 

(A4.43)

 

Ненулевые члены составляющего тензора

 

 

Обратите внимание, что, в случае цилиндрических координатах, общая постановка, которая была подготовлена для извлечения известных выражений различных векторных операторов (градиент, дивергенция, ротор и лапласиан) в этих недекартовских пространственных координатах. Составляющий тензор з зависит от μ и ε (т.е. эффект материала), но и от r (т.е. эффект недекартовых пространственных координат).

 

⇐ Предыдущая38394041424344454647Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: