A 2.4. Стыковка одномодовых волокон

На выходе одномодового волокна псевдо-Гауссова основная мода с радиусом w ₀ на l/ e ² дифрагирует в свободном пространстве в форме расходящегося псевдо-Гауссовского луча, заходящего далеко с углом расхождения на l/ e ² (Рисунок A2.9):

 

Рисунок A2.9. Дальнее поле одномодового волокна с коллимационным объективом

Волокно

Линза

 

(A2.31)

 

Поскольку в пределах практического использования угол расхождения составляет около констант:

(A2.32)

 

Учитывая обратное распространение свободного пространственного гауссовского пучка, сходящегося с углом в целенаправленное гауссовского пятно с тем же радиусом w ₀, можно полностью стыковать с волокном, если ядро центрировано на входящий луч. Чтобы получить такой сходящийся луч, параллельный гауссовский лазерный луч света диаметром 2 w на l/ e ² сфокусирован собирающей линзой с фокусным расстоянием f_l таким как:

 

(A2.33)

 

Снижение несоосности коэффициента сцепления можно рассчитать с общим перекрытием между вводимой волной и основной модой. Вводимая волна может быть разложена на множестве собственных векторов, которые включают уникальные направляемые моды, нормализованные с основными модами и излучающими модами

 

(А2.34)

 

Координаты x_f рассчитываются из обобщенных скалярных произведений:

(A2.35)

Мощность или интенсивность коэффициентов сцепления C это отношения между обобщенными скалярными квадратами , которые пропорциональны мощности сцепленной волны и общему скалярному квадрату , который пропорционален мощности на входе волны:

 

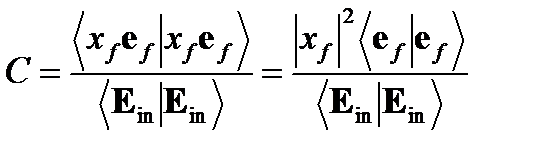(A2.36)

 

(A2.37)

 

Фазовый член может быть ликвидирован в этом обобщенном скалярном произведении, а отношение мощности сцепления определено с перекрытием интегралов переноса распределенного поля:

 

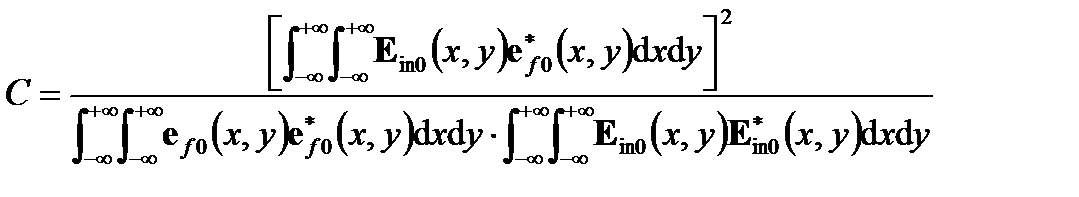(A2.38)

 

Чтобы вернуться к аналогии с геометрическим трехмерным пространством, основные моды аналогичны собственным векторам, и входная волна эквивалентна вектору U. Сцепленный свет в волокне эквивалентен проекции U на ось собственного вектора а _i для получения прогнозируемого вектора:

 

(A2.39)

 

Сцепленная мощность эквивалентна квадрату длины U _p и отношение мощности сцепления эквивалентно квадрату косинуса угла между U и a _i:

 

(A2.40)

 

Когда U перпендикулярна или ортогональна a _i, коэффициент сцепления С равен нулю.

Теперь с аппроксимацией гауссовских мод это отношение сцепления мощности могут рассчитываться с использованием интеграла

 

(A2.41)

 

Результаты часто приводятся в децибелах с потерями в сцеплении Г, определяемыми как:

 

Заметим, что проблема сцепления свободного пространственного сходящегося Гауссова пучка света с одномодовым волокном идентична проблеме соединения двух одномодовых волокон с гауссовскими основными модами. Есть несколько видов перекосов, которые дают потери сцепления (Рисунок A2.10):

• Поперечная несоосность в поперечной (x, y) плоскости:

 

(A2.42)

 

• Продольный сдвиг d_// в направлении распространения z:

 

(A2.43)

 

Угловое смещение

(A2.44)

 

Рисунок A2.10. Потери, вызванные несоосностями: (а) поперечной; (b) продольной; (c) угловой

Обратите внимание, что поперечное и угловое смещения приносят такие же права потерь с отношением радиуса моды w ₀ на 1/ e ² и отношением половины угла расхождения на 1/ e ² соответственно, поскольку проблему углового смещения можно считать проблемой "поперечного смещения" между «виртуальным» Гауссианом удаленных полей.

Принимая снова численный типичный пример высокоапертурного волокна для 850 нм (λ _c = 750 нм, NA = 0,16, = 0,24 рад, 2 а = 3,6 мкм, 2 w ₀= 4,5 мкм), есть 0,5 дБ (или 10%) потери для:

•

•

•

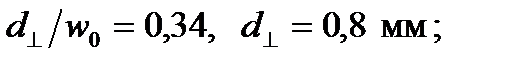
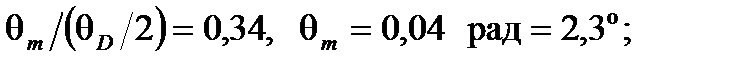
Эти значения получены с "сухим" подключением (т.е. с интерфейсом волокон в воздухе) и 4% (0,2 дБ) потерь Френелевского отражения должны быть добавлены. При подключении с уравненными коэффициентами нет отражения Френеля и расхождение моды в свободном пространстве должно быть заменено в формуле снижения расхождения , в среде с уравненными коэффициентами фактическая длина волны сводится к . Это не меняет поперечный эффект, но эти же 0,5 дБ потери теперь получаются для угловой несоосности или для продольного сдвига d _// = 1,45×12 мкм = 17,5 мкм. Как видно из этого численного примера, механические допуски поперечного выравнивания очень трудны, но продольное и угловое выравнивание требует меньшего сравнения.

Еще одним источником потерь сцепления является несоответствие диаметров мод двух различных волокон, или волокна и интегрального оптического волновода или волокна и гауссовского фокусированного луча. Результат также выводится из перекрытия интегралов, которые можно легко рассчитать с гауссовскими режимами. Несоответствие между двумя диаметры и 2 w ₀ и 2 w' ₀ на 1/ e ² дает;

(A2.45)

 

(A2.46)

 

потеря 0,5 дБ (или 10%), вызванна соотношением диаметров w ₀/ w ₀'=1,4, которое показывает, что допуск на диаметр не очень важен для одномодовых волокон.

В случае эллиптических гауссовских мод амплитуды мод могут быть написаны

(A2.47)

 

где w _{0 x} и w _{0 y} – полуширины на 1/ e ² вдоль мелкой и крупной осей вместо радиуса w ₀, а также потери вследствие несоответствия ширины

 

(A2.48)

 

Обратите внимание, что при сцеплении эллиптической моды с циркулярной наиболее низкие потери получаются, когда радиус w ₀ циркулярной моды равен геометрическому среднему значению половины ширины эллиптической моды:

(A2.49)

 

Например, с эллиптической, если , то w ₀ является оптимальной, когда и потери только 2 дБ. С отношением 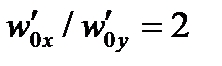оптимальные потери только 0,5 дБ, с . Эти результаты для эллиптических мод полезны не только для определенных волокон, которые могут иметь эллиптические ядра, но и при сцеплении с полупроводниковыми диодами, которые обычно имеют очень эллиптическую форму излучения.

Этот полный анализ сцепления с одномодовым волокном принимаемой входной волны, которая пространственно когерентна; то есть фазы во всех точках поперечной плоскости равны, или по крайней мере коррелированы. Пространственно некогерентный источник не может эффективно сочетаться с одномодовым волокном.

Примечание: Этот анализ сцепления основных псевдо-Гауссовых LP₀₁ мод может быть продолжен для случая моды второго порядка LP₁₁ "псевдо-Гауссовой-производной". Мы видели, что важным преимуществом гауссовской функции является инвариантность от преобразования Фурье ( и 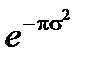образуют пару преобразования Фурье), но гауссовская производная имеет аналогичные свойства.

Фактически с использованием производных теоремы преобразования Фурье это показало, что преобразование Фурье производной есть . Это означает, что когда мода LP₁₁ дифрагирует на выходе из волокна, формы ее расходящегося в свободном пространстве луча сохраняют тот же артисимметричный Гауссиан- производный профиль (Рисунок A 2.11). Заметим, однако, что инвариантность еще не завершена, поскольку дополнительные i -е составляющие указывают, что преобразованием Фурье реальной нечетной функции является исключительно мнимая нечетная функция. Оптически это дает дополнительных π/2 фазовый сдвиг, называемый Guoy эффект, на выходе волны, так как она дифрагирует в свободном пространстве.

Рисунок A2.11. Дальнее поле LP11 моды

Дальнее поле

Луч «псевдо-Гауссовой-производной», который расходится в свободном пространстве, следует течению, похожему на гауссовский луч с полуширинными максимально w' (z):

 

(A2.50)

где 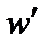– полуширина максимальной моды, а – полный угол расхождения между обоими экстремумами:

(А2.51)

 

Наконец, существует возможность вычислить потери сцепления моды LP₁₁ между двумя волокнами. В частности ширина несоответствие дает интенсивность коэффициента сцепления:

 

(A2.52)

 

Обратите внимание, что эта формула аналогична той, которая для основной моды, но в четвертой степени вместо второй.

 

⇐ Предыдущая34353637383940414243Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: