A 4.2. Электромагнетизм во вращающейся системе отсчета

С математической точки зрения тензорный формализм, полученный в предыдущем разделе, может быть применен к каким-либо координатам; но мы должны определить, с точки зрения физики, какие координаты на самом деле могут быть использованы. С учетом данной системы отсчета координаты должен быть измеримыми с внутренними экспериментами относительно этой системы отсчета. Для перевода хорошо известно, что новые координаты должны быть получены с преобразованием Лоренца. Преобразование Галилея действует математически, но оно дает новые координаты, которые не могут быть измерены во внутренних экспериментах в новой системе отсчета.

В случае вращения со скоростью Ω новые координаты могут быть получены с эквивалентным преобразованием Лоренца, где касательная скорость r Ω заменяет v_t:

(A4.44)

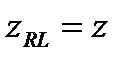
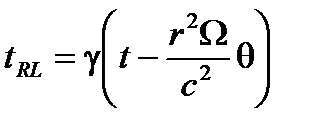
c

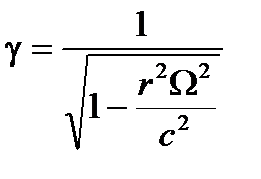
Локально это преобразование является допустимым, и потенциал 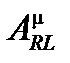, поле 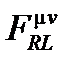и полученное поле 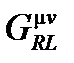определены с этими координатами, соответствующими местным значениям, особенно в покоящейся среде в этой вращающейся системе отсчета. В такой неподвижной среде составной тензор 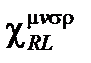равен составному тензору 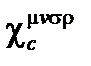, найденному в инерциальной системе отсчета с использованием цилиндрических пространственных координат.

Тем не менее, угловые координаты периодические, и, если принята во внимание вращающаяся система отсчета, эта периодичность появится в координате времени. Для анализа глобальных экспериментов по измерению разности фаз в кольцевом интерферометре Саньяка, координата времени должна быть однозначной и таким образом независимой периодической угловой координатой, и могут быть использованы преобразования Галилея:

 

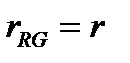
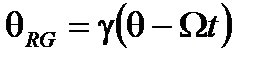(A4.45)

 

В противоположность случаю перемещения эти новые координаты можно измерить во вращающейся системе отсчета. Часы на оси вращения имеют то же самое время, как и время t в инерциальной системе отсчета, и оно может синхронизироваться с временем в целом вращающейся системы, посылая цилиндрические волны, которые распространяются перпендикулярно перемещению и таким образом не изменяются. Угол 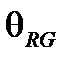может быть определена как постоянная часть полного угла (т.е. 360 град), который по-прежнему очевидно постоянный.

После этого предположения о действии преобразования Галилея для вращения может применяться общий тензорный формализм. В частности, распространение уравнения потенциала в вакууме с четырехмерным формализмом

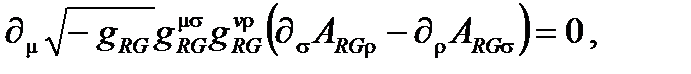(A4.46)

 

где 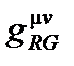– метрический тензор, отвечающий за контравариантные координаты 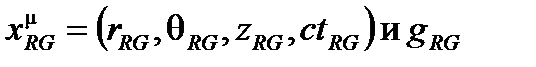и его детерминанты. Имеем

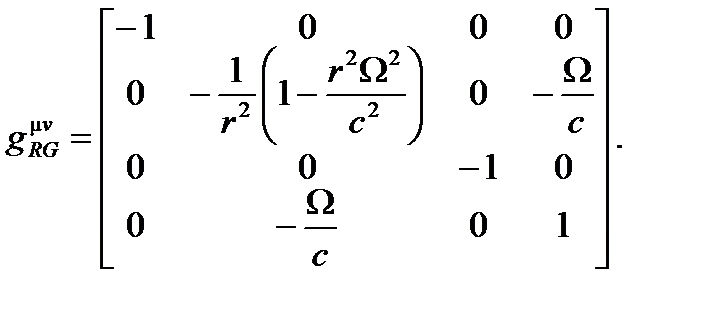(A4.47)

 

Как можно увидеть, есть два недиагональных члена , которые дают различие скоростей распространения между волнами в направлении и против направления вращения. Получаем уравнение распространения в вакууме первого порядка в .

 

(A4.48)

 

где амплитуда волны A для любого компонента поля или потенциала. По сравнению со знакомым уравнением распространения в инерциальной системе отсчета есть дополнительный скрещенный член 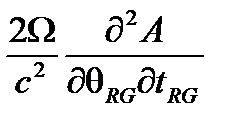, который изменяет скорость волны пропорционально Ω.

В среде по направлению вращения уравнение распространение имеет четырехмерный формализм:

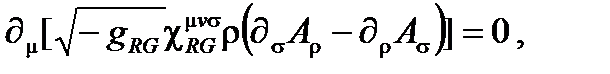(A4.49)

 

где составной тензор 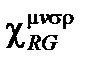заменяет . Этот составной тензор будет рассчитываться с составным тензором в инерциальной системе отсчета с использованием цилиндрических координат и законов преобразования координат между и . Получаем уравнение распространения первого порядка в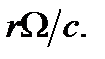

 

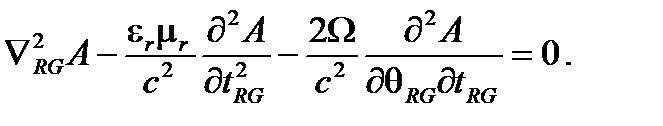(A4.50)

 

Это очень важно отметить, что если ε _r и μ _r, появляются на их обычных местах с 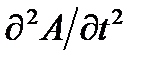, ни один из них не отображается в дополнительном члене 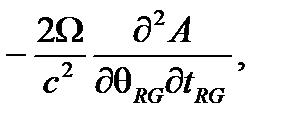который остается идентичным случаю в вакууме. Изменение скорости волны во вращающейся системе отсчета называется эффектом Саньяка, не зависящим от свойств co-вращающейся среды, в которой распространяется свет.

Примечание: С этим релятивистским формализмом становится ясно, что H и D, включенные в уравнения Максвелла М₃ и M₄, связаны, поскольку они составляют контравариантный тензор 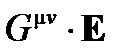и В представляют собой основные поля, производные от потенциал и включение в первые два уравнения Максвелла M₁ и M₂, которые не зависят от вещества. Они образуют ковариантный тензор 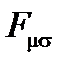и производный тензор поля 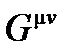, связанный с 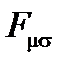, с составным тензором , который учитывает не только свойства материала, но и свойства системы отсчета.

 

⇐ Предыдущая38394041424344454647Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: