 |
A 4.3. Случай вращения тороидального диэлектрического волновода
|
|
|
|
Случай волоконного гироскопа может быть проанализирован более точно с учетом тороидального диэлектрического волновода, где R – радиус кривизны и радиус ядра (Рисунок А 4.3). Как уже было показано (приложение 2), приблизительное решение основной моды прямого волокна – это мода псевдо-Гауссиана с амплитудой:
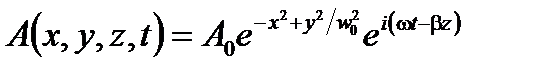 (A4.51)
(A4.51)
| Рисунок A 4.3. Тороидальный волновод |

Когда волокно согнуто, пространственное распространение члена β z может быть заменено на  и наблюдается центрифужный сдвиг
и наблюдается центрифужный сдвиг  моды. Амплитуда моды становится
моды. Амплитуда моды становится
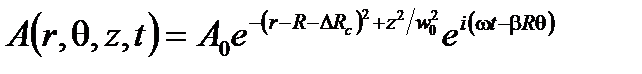 (A4.52)
(A4.52)
с
 (A4.53)
(A4.53)
С помощью метода возмущенности амплитуда во вращающейся системе отсчета с со-вращающимся волоноводом установлена
 (А4.54)
(А4.54)
Есть дополнительный радиальный сдвиг Δ RR вследствие вращения. Это зависит от относительного направление распространения и вращения через сигнатуру (sign) произведения β·Ω:
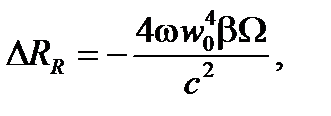 (A4.55)
(A4.55)
но на практике это совершенно незначительно (с типичными параметрами волокна  ). Возмущенностью
). Возмущенностью  на константу распространения является
на константу распространения является
 (А4.56)
(А4.56)
Его относительное значение  также очень мало, но когда волокно помещается в кольцевой интерферометр, есть измерения абсолютной разности фаз между двумя противоположными путями 2π рад, и это накапливается с длиной пути распространения. После N оборотов противораспространенность с соответствующими константами распространения
также очень мало, но когда волокно помещается в кольцевой интерферометр, есть измерения абсолютной разности фаз между двумя противоположными путями 2π рад, и это накапливается с длиной пути распространения. После N оборотов противораспространенность с соответствующими константами распространения 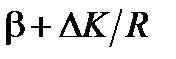 и
и  , разность фаз становится
, разность фаз становится
 (A4.57)
(A4.57)
 (A4.58)
(A4.58)
Этот результат, известный как эффект Саньяка, зависит только от частоты света ω, скорости света в вакууме с и общей площади, заключенной в катушке  . Значения ядра и оболочки, фазовой или групповой скоростей мод и дисперсия среды или волновода не имеют влияние.
. Значения ядра и оболочки, фазовой или групповой скоростей мод и дисперсия среды или волновода не имеют влияние.
|
|
|
Эффект Саньяка – чистая временная задержка, не зависящая от материи, которая измеряется "часами" частотой источника света. Однако поскольку длина волны λ в вакууме более привычное количество, чем частота для оптических волн, формула обычно записывается
 (A4.59)
(A4.59)
где D = 2 R диаметр петли и L = N 2π R – общая длина волновода навиваемого из N витков.
Библиография
О теории относительности и электродинамике:
• Tonnelat, м. а., Принципы теории электромагнетизма и теории относительности, Гордон и нарушение, 1966.
• Ландау, л. д. и е. м. Липшицевость, Классическая теория поля, Пергамский пресс. 1975 Г.
• Arzelies, х., Cinematique Relativiste, на французском языке, Готье Вилларе, 1955 г.
О теории электромагнетизма эффекта Саньяка:
• Пост, е. ю., "Эффект Саньяка" Обзор современной физики, том 39, 1967 года, стр. 475-493.
• Пост, е. J.F "Изменение интерферометрической длины пути вследствие движения," журнала оптический общества Америки, Vol. 62, 1972, pp. 234-239 (SP1E MS8, pp. 79-84).
• Arditty, н. д. и н. с. Лефевр, "Теоретические основы эффекта Саньяка в волоконном гироскопе," Springer Verlag серии в оптический наук, Vol. 32, 1982 г., стр. 44-51.
• Лефевр, II. С и н. я. Ardilty, "Eleclromagnelisme des кругах dieleclriques lineaires en вращения et приложение a la распространения d'ondes guidees," по-французски, прикладной оптики, том 21, 1982, pp. 1400-1409.
Символы
| A(t) | Амплитуда оптической волны | |
| A µили A µ | Электромагнитные четырехпотенциальные координаты | |
| A | Вектор электромагнитного потенциала | |
| A | Площадь | |
| A | Вектор площадки | |
| a | Радиус ядра волокна | |
| ae | Радиус ядра эквивалентного шага индекса волокна | |
| ah | Размер пространственного фильтрующего отверстия | |
| a(f) | Частота компонентs A (t) | |
| В | Константа двулучепреломления | |
| В | Вектор магнитного поля | |
| b (V) | Стандартная константа переноса | |
| С | Коэффициент связи мощности | |
| с | Скорость света в вакууме (2,998·108 м·с-1) | |
| c (z) | Случайная поляризационная связь вдоль волокна | |
| сs | прочность связи в кратковременном поле соединителя | |
| curl | Оператор ротора | |
| D | Диаметр | |
| D | Вектор производной электрического поля | |
| d | Расстояние или толщина | |
| div | Оператор дивергенции | |
| E | Модуль Юнга | |
| E {} | Ансамбль в среднем | |
| E | Вектор электрического поля | |
| e | exp (1) = 2.7183... | |
| el | Эллиптический | |
| F µ v или F µ | Тензор электромагнитного поля | |
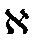
| Утонченность оптической полости | |
| f | Временнáя частота | |

| Средняя временнáя частота | |

| Фокусное расстояние | |

| Частота модуляции | |

| Основная или собственная частота катушки | |
| f | Сила | |
| G µ v или G µ v | Производная тензорного поля | |
| g u v или g u v | Метрический тензор | |
| grad | Оператор градиента | |
| H | Вектор напряженности магнитного поля | |
| НЕ11 | Фундаментальная смешанная электромагнитная мода | |
| h | Постоянная Планка (6,63·10–34 Дж·с) | |
| h | h–параметр сохранения поляризации волокна | |
| I | Интенсивность оптической волны | |
| i | Сила электрического тока | |
| i | Значение мнимой единицы | |
| Jn | Функция Бесселя порядка n | |

| Четырехкомпонентный электрический ток | |
| j | Вектор плотности электрического тока | |
| k | Постоянная Больцмана(1,38·10–25 Дж·К–1) | |
| k 0 | Волновое число в вакууме | |
| k 1 | Волновое число в ядре | |
| k 2 | Волновое число в оболочке | |
| km | Волновое число в среде | |
| L | Длина | |
| Lbb | Общая базово-ответвленная длина | |
| Lc | Длина когерентности | |
| Lcp | Длина связи | |
| Lop | Оптическая длина пути | |
| Lp | Длина пульсации | |
| Lpc | Длина корреляции поляризации | |
| LP 01 | Основная линейно поляризованная мода | |
| LP 11 | Второй порядок линейно поляризованной моды | |
| LSB | Наименьший важный бит | |
| M | Вектор магнитной поляризации | |
| M (t) | Модуляция сигнала | |
| N | Количество поворотов | |
| NA | Числовая апертура | |
| n | Показатель преломления | |
| n 1 | Показатель преломления ядра | |
| n 2 | Показатель преломления оболочки | |
| no | Показатель преломления обыкновенный | |
| ne | Показатель преломления необыкновенный | |
| neq | Эквивалентный показатель преломления | |
| P | Мощность | |
| P | Вектор электрической поляризации | |

| Периметр | |
| Р | Степень поляризации | |
| p | давление | |
| p | параллель (поляризации) | |
| pij | Упруго-оптическиt коэффициенты | |
| ppm | части на миллион | |
| q | заряда электрона | |
| R | Радиус | |
| R | Cопротивление | |
| Rc | автокорреляция (ансамбль в среднем) | |
| Rf | Радиус оболочки волокна | |
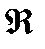
| Отражательность | |
| r | Радиальная координата | |
| r | Радиальный вектор | |
| rij | Электро-оптические коэффициенты | |
| rms | Значение квадратного корня | |
| S | фактор рецептуры | |
| s | перпендикулярно (поляризации) | |
| T | Температура | |
| Ta | Абсолютная температура | |
| TС | Температура Кюри | |
| Tm | Период фазовой модуляции | |
| Tn | Нормальное напряжение | |
| Tnс | Сжимающее напряжение | |
| ТЕ | Поперечная электрическая мода | |
| TM | Поперечная магнитная мода | |
| t | Время | |

| Удельный коэффициент пропускания | |
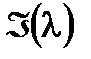
| Удельный коэффициент пропускания фильтра с длиной волны | |
| V | нормализованная частота в волноводе | |
| V | Электромагнитный скалярный потенциал или напряжение | |
| V | Коэффициент Верде | |
| v | Скорость света в среде | |
| v | Быстрота или скорость | |

| Видимые полосы интерференции | |
| w | Радиус 1/ e 2 в интенсивном гауссовском излучении | |
| w 0 | Радиус 1/ e 2 в суженной части интенсивного гауссовского излучения или радиус 1/ e 2 псевдогауссовой основной LP01 моды | |
| w 1 | Половина ширины максимума LP11 моды | |
| x,y,z | Декартовые пространственные координаты | |
| xj | Координата | |
| Z | Импенданс | |
| Z 0 | Импенданс в вакууме | |

| Затухание на единице длины волокна | |

| Модуль от а (f) | |

| Коэффициент Физо в градусах | |

| Константа передачи | |
| Г | Потеря связи | |

| Автокорреляционная функция (усредненная по времени) | |

| 
| |

| Нормированная автокорреляционная функция (усредненная по времени) | |

| Нормированный индекс разности | |

| Нормированный индекс разности эквивалентный индексу шага волокна | |

| Разность от | |

| Разность частот с шагом назад | |

| Полная ширина половины максимума временного спектра частот | |

| Разность частот, вызванная вращением | |

| Ширина полосы пропускания счетчика | |
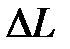
| Геометрическая разность хода | |

| Оптическая разность хода | |
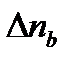
| Разность показателей двулучепреломления | |

| Двулучепреломление | |

| Разность фаз | |
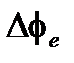
| Ошибка разности фаз | |

| Разность фаз, индуцируемая эффектом Фарадея | |
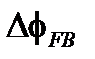
| Разность фаз с шагом назад | |

| Разность фаз, индуцируемая эффектом Керра | |

| Модуляция от разности фаз | |

| Разность фаз, индуцируемая наклоном фазы | |
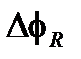
| Разность фаз, индуцируемая вращением из-за эффекта Саньяка | |

| Полная ширина половины максимума спектра длин волн | |
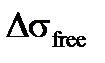
| Свободный спектральный диапазон оптического резонатора | |

| Разность времен группового переноса через катушку | |

| Вариация или сдвиг | |

| Вариация показателя преломления | |

| Сдвиг фазы | |

| Малый коэффициент | |

| Диэлектрическая проницаемость в вакууме (8,854·10–12 Ф/м) | |
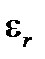
| Диэлектрическая проницаемость среды | |

| Угол | |

| Угол Брюстера | |

| Полное угловое расхождение при 1/ е 2 Гауссова пучка в вакууме | |

| Полное угловое расхождение при 1/ е 2 Гауссова пучка в среде | |

| Предельный угол полного внутреннего отражения | |
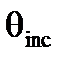
| Угловое приращение гироскопа | |

| Двулучепреломление при пульсации длины | |

| Длина волны в вакууме | |

| Средняя длина волны | |

| Усеченная длина волны | |
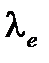
| Длина волны излучения | |

| Длина волны в среде | |

| Магнитная прницаемость в вакууме (4π·10–7 Гн/м) | |
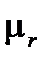
| Магнитная прницаемость в среде | |

| Коэффициент Пуассона | |

| Вектор Пойнтинга | |
| π | 3,14159… | |

| Плотность электрического заряда | |

| Перекрестное соединение интенсивности поляризации | |
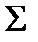
| Суммирование | |

| Пространственная частота | |

| Усредненная пространственная частота | |

| Значение среднеквадратичного отклонения | |
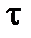
| Временная задержка | |

| Время когерентности | |

| Время декогерентности | |

| Групповая задержка | |

| Задержка фазы | |

| Фаза | |

| Наклон | |

| Смещение фазы | |
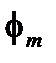
| Фазовая модуляция | |
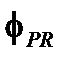
| Наклон фазы | |

| Шаг фазы | |

| Диэлектрическая проницаемость | |
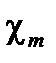
| Магнитная восприимчивость | |

| Конститутивный тензор | |

| Скорость вращения | |

| Вектор скорости вращения | |

| Скорость вращения, индуцируемая разность фаз в π радиан | |

| Скорость вращения, индуцируемая разность фаз в 1-µ радиан | |

| Циклическая частота | |

| Усредненная циклическая частота | |
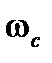
| Циклическая частота излучения | |

| Временное осреднение | |

| Обобщенное скалярное произведение сложных функций | |

| Абсолютное значение | |

| Векторный дифференциальный оператор | |
|
|
|
|
|
|
|
|
|
Об авторе
Эрве C. Лефевр является вице-президентом исследований и разработок для «Photonetics» во Франции. Он родился в 1954 году в Париже, Франция. Окончил «Ecole Normale Superieure де Сен Клуд», получил Agregation по физики в 1976 году, доктора 3-го цикла в 1979 году и доктора «d'Etat» в 1982 году.
Он начал работать на волоконно-оптический гироскоп в 1977 году как ученый – выпускник Центральной научно-исследовательского лаборатории «Thomson-CSF» во Франции, и в период 1980-1982 года он занимался исследованиями в постдокторантуре Стэнфордского университета. Затем он возвратился в «Thomson-CSF» как ученый исследователь и стал заведующим лабораторией волоконно-оптических датчиков в 1984 году. В 1987 году он присоединился к «Photonetics», которая является компанией, специализирующейся на волоконно-оптических датчиках и фотонных инструментариях.
|
|
|
Он является автором и соавтором публикаций о волоконно-оптическом гироскопе и соответствующих технологиях в почти 50-ти журналах и конференциях, им было предоставлено 25 патентов. Он был награжден премиией «Fabry-de Gramont» в 1986 году французским Обществом оптики и премией «Esclangon» в 1992 году французского общества физиков.
|
|
|


