 |
Классическое определение вероятности
|
|
|
|
Прежде, чем подойти к определению вероятности, рассмотрим опыт, состоящий в бросании игральной кости. Очевидно, что события A 1 = {выпало 1 очко},..., A 6 = {выпало 6 очков} равноправны, т.к. имеют одинаковые возможности произойти в этом опыте (в силу симметрии кубика).
Элементарные события называются равновозможными, если любое из них не имеет преимуществ по отношению к другим событиям появляться чаще других.
В качестве примера равновозможных можно назвать события A = {выпал герб} и В = {выпала решка} при однократном подбрасывании одной монеты.
Событие называется благоприятным (или благоприятствующим) некоторому событию, если его появление влечет за собой появление данного события.
Так, при одном бросании кубика событию A = {выпало нечетное число очков} благоприятствуют 3 события: A 1, A 3, A 5.
Событием, противоположным событию A, называется событие 
, которое наступает тогда и только тогда, когда не наступает A.
Например, при подбрасывании одной монеты событие A = {выпал герб} противоположно событию 
= {выпала решка}.
Вероятностью случайного события A называют отношение числа благоприятствующих этому событию элементарных событий к числу всех равновозможных несовместных элементарных событий, образующих полную группу
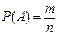, (1)
где, m – число исходов, благоприятствующих событию A,
n – общее число исходов.
Свойства вероятности события
1. Вероятность достоверного события U равна единице:
P (U) = 1.
2. Вероятность невозможного события V равна нулю:
P (V) = 0.
3. Вероятность любого события заключена между нулем и единицей:
0 ≤ P (A) ≤ 1.
Пример 1. Шесть одинаковых карточек, на которых написаны буквы Р, Т, Е, О, Я, И, разложили наудачу в ряд. Какова вероятность того, что получится слово ТЕОРИЯ?
|
|
|
Решение. Пусть событие А = {получится слово ТЕОРИЯ}. Общее число исходов равно числу всевозможных перестановок из 6 букв, т.е. n = 6! Из данных букв слово ТЕОРИЯ можно составить только одним способом, следовательно, существует один благоприятный исход. Используя формулу (1), получим
.
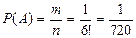Пример 2. Бросают 2 монеты. Какова вероятность того, что выпадут 2 герба?
Решение. Пусть событие А = {выпадет 2 герба}. В результате опыта возможны 4 исхода: {г; г}, {г; ц}, {ц; г}, {ц; ц}, т.е. n = 4. Событию A благоприятствует только один исход {г; г}, т.е. m = 1.
Отсюда P (A) = 1/4.
Пример 3. В ящике лежат 4 белых, 3 черных и 5 синих шаров. Наудачу вынимаются 6 шаров. Какова вероятность того, что вынуты 1 синий, 2 черных и 2 белых шара?
Решение. Обозначим А = {вынуты 1 синий, 2 черных и 2 белых шара}.
Число всевозможных исходов опыта
n = 
= 792.
Теперь найдем число благоприятных исходов. 1 синий шар из 5 можно выбрать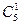 
способами; 2 черных шара из 3 можно выбрать 
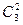способами; 2 белых шара из 4 можно выбрать 
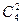способами. Тогда, в силу правила произведения в комбинаторике, общее число благоприятных исходов
m =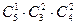 
= 120.
Используя формулу (1), получим
P (A) =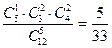 
.
Задачи для самостоятельной работы
1. Монета подбрасывается 2 раза. Найти вероятность того, что:
а) оба раза появится решка;
б) решка появится только один раз.
Отв.: а) 1/4; б) 1/2.
2. Найти вероятность того, что при бросании трех игральных костей шестерка выпадает на одной кости, если на гранях двух других костей выпадет различное число очков (не равное шести).
Отв.: 
= 1/2.
3. Из букв разрезной азбуки составлено слово СТАТИСТИКА. Затем из этих букв случайным образом без возвращения отобрано 5 букв. Найти вероятность того, что из отобранных букв можно составить слово ТАКСИ.
Отв.: 2/21.
4. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся:
|
|
|
а) одно окрашенное изделие;
б) два окрашенных изделия;
в) хотя бы одно окрашенное изделие.
Отв.: а) 
= 0,6; б)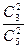 
= 0,3; в) 0,9.
|
|
|
