 |
1.8.1. Связь собственной энергии молекулы μi в среде с парным потенциалом W(r)
|
|
|
|
1. 8. 1. Связь собственной энергии молекулы μ i в среде с парным потенциалом W(r)
Собственная энергия молекулы μ i в среде – сумма взаимодействий молекулы со всеми окружающими молекулами.
Газовая среда:
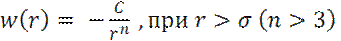- потенциал парного взаимодействия
, при r < σ
σ – диаметр твердой сферы молекулы.
Расчет собственной энергии μ i молекулы i суммированием всех парных потенциалов W(r) по всему пространству:
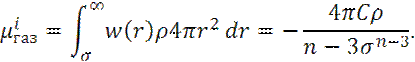
Здесь ρ – число молекул в единице объема.
Жидкая среда:
При введении новой молекулы в раствор рвутся старые связи и образуются новые. При этом, полное изменение энергии равно:
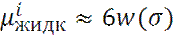
Где W(σ ) – парный потенциал двух молекул, находящихся в контакте при r = σ.
Молярная собственная энергия U молекул i в растворе составляет:
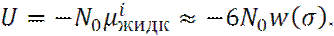
Где N0 – число Авогадро.
В чистой жидкости числовая плотность ρ молекул равна:
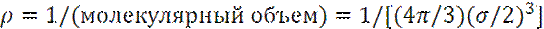
Таким образом, для собственной энергии μ i молекулы i в растворе получаем:
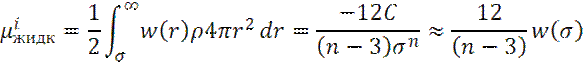
Для ван-дер-ваальсова взаимодействия (n=6), это дает:
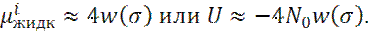
Парный потенциал между двумя растворенными молекулами вещества есть просто изменение суммы их свободных энергий μ i, по мере того, как они сближаются.
1. 9. Распределение Больцмана
Пусть имеются две равновесные области, в которых молекулы сорта i имеют собственную энергию μ i1 и μ i2.
Тогда равновесные концентрации молекул сорта i будут связаны хорошо известным распределением Больцмана:
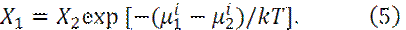
Или
Величина μ известна, как химический потенциал.
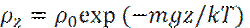- Барометрическое распределение
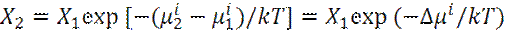- Растворимость по Нернсту
1. 10. Оценка параметров a и b уравнения состояния Ван-дер-Ваальса с позиций микроскопического рассмотрения
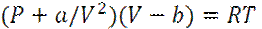Уравнение состояния Ван-дер-Ваальса
|
|
|
Пусть молекулы газа взаимодействуют с потенциалом парного притяжения
(6)
Тогда, собственная энергия μ i2 молекул в газе может быть записана, как:
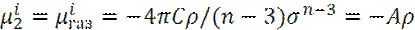
Где
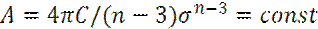
Учитывая конечные размеры молекул, можно записать:
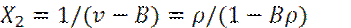
где v – газовый объем на одну молекулу;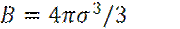 
σ – расстояние, на которое одна молекула может подойти к другой.
Теперь, для химического потенциала μ газа, имеем:
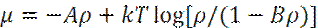
Согласно фундаментальному уравнения Гиббса
где: E - энергия системы; Т – температура; S – энтропия системы; P, V – давление и объем системы, μ – химический потенциал; N – число частиц в системе.
Или
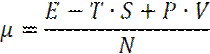
Отсюда получаем:
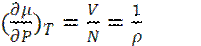или 
Определим частную производную (∂ P/∂ ρ ), рассматривая давление P, как сложную функцию:
Теперь:
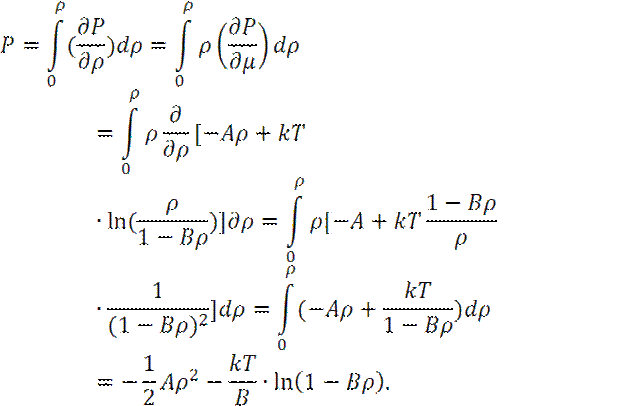
При выводе последнего соотношения учитывалось, что:
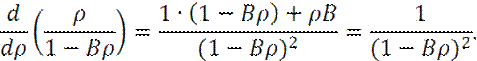
Теперь учтем разложение ln(1+x) в ряд Тейлора:
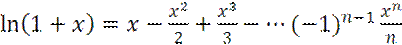+…, x 
]-1; 1]
с точностью до третьего члена, т. е.:
Разложим логарифмический член в (7) в ряд:
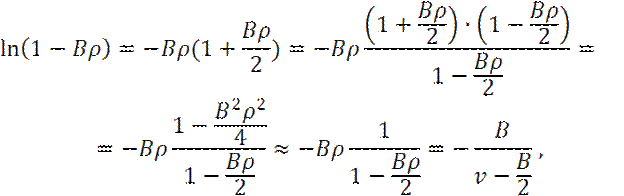
Так, как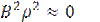 
и ʋ - мольный объем системы.
Тогда получим:
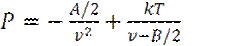или 
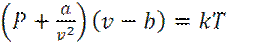(8)
Уравнение (8) есть уравнение состояния Ван-дер-Ваальса, в терминах молекулярных параметров σ, n и С.
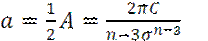и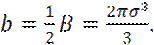 
Концептуально, константы a и b соответствуют силам притяжения и отталкивания.
Контрольное задание
Используя зависимость потенциала Ленард-Джонса W(r), от расстояния между атомами (молекулами) r, нарисовать примерный ход графика зависимости силы взаимодействия F, двух атомов (молекул), в зависимости от расстояния между ними r.
Глава 2. РОЛЬ СТАТИСТИЧЕСКОЙ МЕХАНИКИ В МОДЕЛИРОВАНИИ НАНОСИСТЕМ
1. Компьютерное моделирование позволяет рассчитать поведение каждой частицы системы (моделирование жидкой воды, методом МД – координаты, скорости).
2. Величины, измеренные в эксперименте не соответствуют рассчитанным, так, как они усреднены по ансамблю частиц и времени;
3. В типичном эксперименте измеряются величины, усредненные по большому числу частиц и усредненные за время измерения;
|
|
|
4. Для использования результатов компьютерного моделирования надо знать какого типа средние величины необходимо вычислять в ходе компьютерного эксперимента;
5. Для этого, необходимо перейти на язык статической механики.
|
|
|
