 |
2.1. Статистическое определение энтропии и температуры системы частиц
|
|
|
|
2. 1. Статистическое определение энтропии и температуры системы частиц
1. Основное допущение компьютерного моделирования наносистем: законы классической механики применимы для описания движения атомов и молекул;
2. Основные законы статической механики проще получить, используя квантовую механику (как ни странно);
3. Квантово-механическая система с заданным числом частиц, объемом и энергией может находиться в разных состояниях;
4. Будем рассматривать квантовые состояния системы, которые являются собственными векторами гамильтониана Н системы, т. е. собственными состояниями по энергии. Гамильтониан определяется, как квантовый оператор, соответствующий сумме кинетической К и потенциальной U энергии квантовой системы;
5. В квантовой механике состояние системы i обозначается символом |i > (брекет)
6. Таким образом, для любого состояния |i >, имеем:
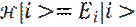(1)
Где Ei – полная энергия системы, в состоянии |i >.
7. Обозначим через Ω (N, V, E) число собственных состояний с энергией Е системы N частиц в объеме V.
8. Основной постулат статической механики:
Система с фиксированными N, V, E, с равной вероятностью может быть найдена в одном из своих собственных состояний Ω (E).
9. Рассмотрим систему с полной энергией Е, которая состоит из двух слабовзаимодействующих подсистем:
10. Есть много способов распределения полной энергии по двум подсистемам, таких, что E1+E2=E.
11. Для данного выбора E1, общее число состояний системы с заданной энергией (вырожденные состояния) равно: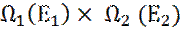 
.
12. Обычно, кратность вырождения системы, в силу аддитивности, выражается, как:
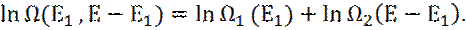
13. Какое будет наиболее вероятное распределение энергии Е между подсистемами 1 и 2? (число микросостояний подсистем очень сильно зависит от Е1).
|
|
|
14. Наиболее вероятное значение Е1 максимизирует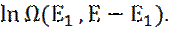 
15. Условие этого максимума записывается, как:
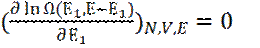(2)
Или:
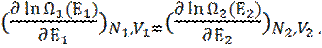(3)
Если обозначить:
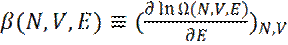(4)
То уравнение (3) примет вид:
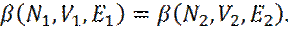(5)
При выполнении условия (3) обе подсистемы будут находиться в тепловом равновесии с максимальным значением lnΩ.
Второй закон термодинамики гласит, что у равновесной системы, энтропия S максимальна. Отсюда, энтропия системы S связана с кратностью вырождения системы Ω, соотношением:
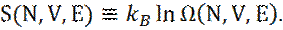(6)
где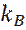 
= 1, 38066 ∙ 10-23 Дж/К – постоянная Больцмана.
При тепловом равновесии температуры подсистем 1 и 2 равны.
При постоянных N, V, T, справедливо термодинамическое соотношение Клаузиуса:
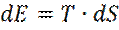
Из последнего соотношения следует термодинамическое определение абсолютной температуры:
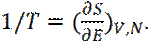(7)
Или:
(8)
Продолжим искать вероятность нахождения подсистемы А с заданной энергией Ei в равновесной системе А-В, с общей энергией Е. Пусть энергия ЕВ теплового резервуара В много больше энергии EA=Ei, подсистемы А.
Тогда, резервуар В, будет иметь энергию Е-Еi, с кратностью вырождения Ω В(Е-Еi).
2. 2. Энергетическое распределение Больцмана
Очевидно, что кратность вырождения резервуара В, определяет вероятность нахождения подсистемы А с энергией Еi.
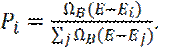(9)
Чтобы вычислить число состояний резервуара B с энергией (E – Ei) разложим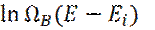 
вблизи Ei=0:
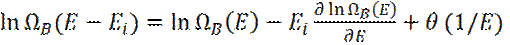(10)
Или, используя уравнения (6), (7):
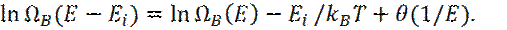(11)
Подставив (11) в (9), получим хорошо известное распределение Больцмана для системы при температуре Т:
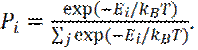(12)
2. 3. Среднее значение энергии системы < E> при температуре Т
Больцмановское распределение системы частиц по энергиям дает возможность определить среднее значение энергии < E> системы при данной температуре Т:
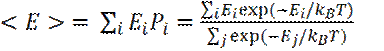(13)
Соотношение (13) можно записать в следующем виде:
(14)
где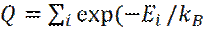 
T) – статическая сумма.
|
|
|
|
|
|
