 |
2.4. Среднее значение <A> наблюдаемой величины А системы наночастиц
|
|
|
|
2. 4. Среднее значение < A> наблюдаемой величины А системы наночастиц
Рассмотрим расчет среднего значения наблюдаемой величины А, с позиций статической механики. Мы знаем вероятность нахождения системы наночастиц в квантовом состоянии, с энергией Еi (через распределение Больцмана). Поэтому, термодинамическое среднее < А> величины А вычисляется, как:
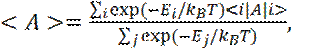(15)
где < i|A|i> - означает математическое ожидание оператора А в квантовом состоянии i.
Необходимость вычисления математического ожидания возникает в силу существования множества подуровней одного и того же уровня Ei.
Чтобы найти < i|A|i> , необходимо решить уравнение Шредингера для каждого квантового состояния системы наночастиц, а затем вычислить математическое ожидание оператора А.
Задача получается абсолютно не решаемая, и поэтому производят упрощение.
Энергию состояния Ei (и, соответственно, гамильтониан системы Н) рассматривают, как сумму кинетической Ki и потенциальной энергии Ui:
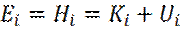(16)
Причем, каждый вид энергии представляют в базисе собственных векторов. Тогда получают следующее классическое выражение для термодинамического среднего, наблюдаемой величины А:
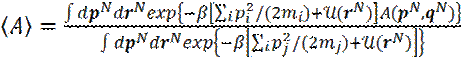. (17)
где p – вектор импульсов наночастиц; r = q – вектор координат наночастиц;
2. 5. Эргодичность системы многих частиц
Основной постулат статической механики наносистем: каждое квантовое состояние может быть занято системой с равной вероятностью.
Тогда, среднее системы частиц определяется, как среднее, по ансамблю состояний системы.
Но в реальном эксперименте мы измеряем какую-либо величину в течение определенного промежутка времени, и в результате получаем среднее значенип за этот промежуток.
|
|
|
Предположим, что мы хотим рассчитать среднюю плотность жидкости, на растоянии r от некоторого атома i – pi(r). С течением времени, координаты атомов меняются и, следовательно, будет меняться плотность вокруг атома i. В методе молекулярной динамики рассчитывается усредненная по времени плотность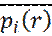 
системы N атомов, в объеме V, при постоянном значении полной энергии Е:
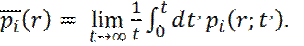(18)
В выражении (18) предполагается, что 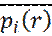не зависит от начальных условий. Тогда, результат для 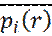не изменится при усреднении по многим различным начальным состояниям, при одних и тех же значениях N, V и E, но с различными начальными координатами и импульсами:
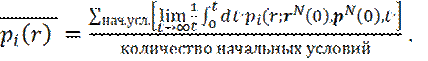(19)
В предельном случае бесконечного количества начальных условий возможно поменять местами усреднение по начальным условиям и усреднение по времени, как не зависящие друг от друга операции.
Тогда обозначая через < … > среднее по начальным условиям (ансамблю), получаем:
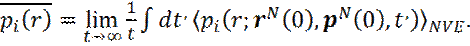(20)
Из уравнения (20) следует, что усреднение по начальным координатам в фазовом пространстве эквивалентно усреднению по времени по траектории в фазовом пространстве.
В связи с этим, можно опустить усреднение по времени в формуле (20) и записать:
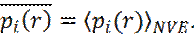
Из последней формулы следует:
- при вычислении средней величины функции координат и импульсов системы многих частиц можно вычислять эту среднюю величину с помощью усреднения по времени (метод молекулярной динамики), либо с помощью усреднения по ансамблю (метод Монте-Карло).
Системы многих частиц, для которых справедливо соотношение (21) называются эргодичными.
|
|
|
