 |
контрольное задание 1. Чему равно число конфигураций в объединенной системе? Вычислить также энтропии s , S1 , S2 . Глава 3. Модели квантовых наносистем
|
|
|
|
Контрольное задание 1.
Рассмотрим систему А, состоящую из подсистем А1 и А2 ,
для которых Ω 1 = 1020 и Ω 2 = 1022 .
Чему равно число конфигураций в объединенной системе? Вычислить также энтропии S, S1 , S2 .
Контрольное задание 2.
Во сколько раз увеличится число доступных конфигураций при расширении на 0, 001% 10 м3 воздуха, при постоянной температуре, находящегося при давлении 1, 0 атм и температуре 300 К?
Уравнение состояния: PV = nRT.
При изотермическом расширении газа в пустоту:
Δ S = nR ln(V2 / V1), т. к. T dS = dU + P dV и PV = nRT.
S = kB ln Ω; kB = 1, 38 10-23 Дж/K; R = 8, 31 Дж/(моль К);
1 атм = 105 Па.
Глава 3. МОДЕЛИ КВАНТОВЫХ НАНОСИСТЕМ
3. 1. История создания квантовой механики
1. 1900 год. Макс Планк решает задачу теплового излучения и предлагает заменить непрерывное множество значений энергии дискретным множеством.
Вводит понятие кванта энергии: h n.
По Планку энергия излучения может принимать значения кратные частоте:
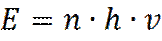
(где n – частота излучения, равная ω /2π ; ω – угловая частота).
Постоянная Планка h = 6, 626•10-34 Дж с. Если пользоваться угловой частотой ω, то постоянная Планка выражается как: ħ = h/2p. При этом выполняется равенство: h n = ħ ω.
2. 1905 год. Эйнштейн выдвигает гипотезу: «Свет также имеет квантовую природу и является потоком световых квантов-фотонов с энергией: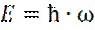 
. »
Согласно, теории относительности: полная энергия E любой частицы, с массой m, движущейся со скоростью v, равна:
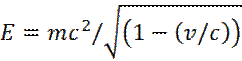(1)
Для фотона: v=c. Отсюда следует, что фотон не имеет массы покоя.
3. 1913 год. Нильс Бор формулирует 2 постулата атомно-молекулярной физики:
1. ) Атомная структура устойчива только для определенной совокупности дискретных стационарных состояний;
|
|
|
2. ) Способность атома (молекулы) поглощать и испускать излучение подчиняется закону: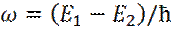 
, (2)
где ω – частота излучения.
Бор предположил, что момент импульса M электрона в атоме водорода равен: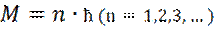 
. (3)
4. 1924 год. Луи де Бройль высказал гипотезу, что соотношение:
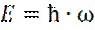, относится не только к фотонам, а имеет универсальный характер и относится ко всем частицам, длина волны λ равна:
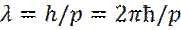(4)
где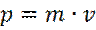 
- импульс частицы.
5. 1927-1932 годы. Джон фон Нейман завершил математическую формулировку квантовой механики на языке гильбертова пространства (линейного векторного, со скалярным произведением).
Элементами этого пространства являются волновые функции, описывающие состояние квантовой системы.
На основе идеи квантования атомной системы, используя постоянную Планка - ħ , массу m и заряд e электрона, удалось вычислить радиус r1, первой орбиты электрона, в теории Бора:
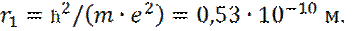(5)
Гейзенберг опубликовал соотношение неопределенности в атомных системах:
1. ) Точность одновременного определения координат и импульса частицы не может превосходить величины ħ : 
;
2. ) Точность определения энергии E, за промежуток времени Δ t, не может превосходить величины ħ :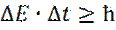 
.
Эти неопределенности связаны с воздействием на объект при измерении.
3. 2. Основные понятия и математический аппарат квантовой механики
В квантовой механике, в силу соотношения неопределенности Гейзенберга, классические определения координат, импульса, энергии частиц теряют смысл.
Вводится волновая функция Ψ (r, t), являющаяся комплексной величиной, позволяющая вычислить остальные характеристики частицы.
Волновая функция - Ψ (r, t), позволяет находить вероятностные характеристики всех параметров микрочастиц.
Квадрат модуля волновой функции | Ψ |2, для элемента пространства, объемом dV, определяет вероятность нахождения микрочастицы в данном объеме:
|
|
|
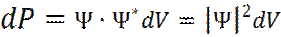(6)
где Ψ * - комплексно-сопряженная волновая функция.
Отсюда, функция плотности вероятности (вероятность нахождения микрочастицы в единице объема) P, будет равна:
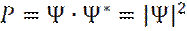(7)
Функция плотности вероятности должна удовлетворять условиям нормировки:
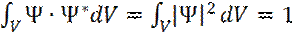, (8)
где интеграл берется по всему пространству, где Ψ ≠ 0.
Теперь, вероятность dP нахождения частицы в интервале (X, X+dX) будет равна: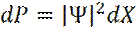 
. (9)
Среднее значение координаты - Xср частицы, определяется как
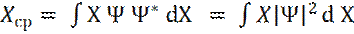(10)
В общем случае, среднее значение любой функции fср(X), находится по аналогичной формуле:
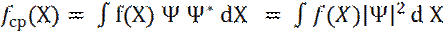(11)
|
|
|
