3.6. Решение уравнения  Шредингера в случае движения свободной частицы вдоль оси X

3. 6. Решение уравнения  Шредингера в случае движения свободной частицы вдоль оси X

 

Уравнение Шредингера в этом случае имеет вид:

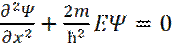   (23)

(Где:  )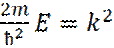

Или:

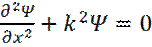   (24)

Уравнение (24) – это обыкновенное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Базисные функции пространства решений этого уравнения есть: exp(λ ₁x) и exp(λ ₂x),

где λ ₁ и λ ₂ - корни следующего характеристического уравнения:

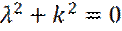   (25)

равные: λ ₁ =0+i k, λ ₂ =0-i k.

Общее решение уравнения (24) есть линейная комбинация базисных функций, т. е.:

Ψ (x) = A exp(0+i k) + B exp(0-i k).

Или с учетом ограничений физического смысла функции Ψ (x) имеем:

Ψ (x) = A exp(ikx)    (26)

Общее решение уравнения с учетом временной зависимости Ψ (x, t), будет:

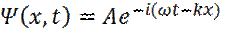   (27)

Или используя формулу Эйлера:

,

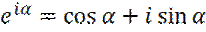Получаем:

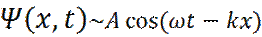 - уравнение плоской волны (28)

Мы ввели обозначение k² = 2mE/ ħ ² .

Отсюда получаем:

   (29)

Т. е. энергетический спектр частицы непрерывный.

Рассмотрим вероятность | Ψ |² нахождения частицы в пространстве:

|Ψ |²=Ψ Ψ ^* = A exp(-i (ω t – kx)) A exp(i (ω t – kx)) =A²= const, (30)

т. е. вероятность найти частицу во всем объеме одинакова.  

3. 7.  Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками

 

 

Частица движется вдоль оси x.

Энергия отсчитывается от дна ямы.

Яма описывается потенциальной энергией:

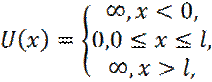 l – ширина ямы.

Уравнение Шредингера для стационарного состояния в одномерном случае:

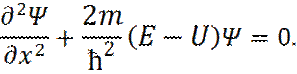
Из граничных условий следует:

1. Бесконечно высокие стенки → частица не проникает за пределы ямы →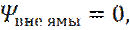

2. На границе ямы 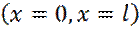 непрерывная функция  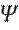обращается в нуль:

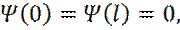
3. В яме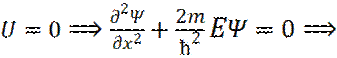

(где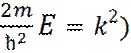

Дифференциальное уравнение гармонического осциллятора:

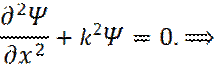
Общее решение дифференциального уравнения:

Условие на границе:

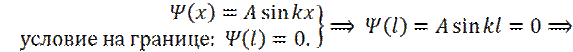
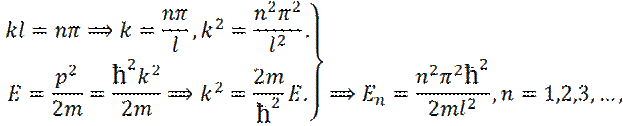
т. е. уравнение Шредингера удовлетворяется только при собственных значениях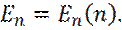

Т. о. 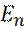 принимает дискретные значения – квантуется. Квантовые значения  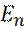называются уровнями энергии.

n – главное квантовое число определяет энергию уровня.

   

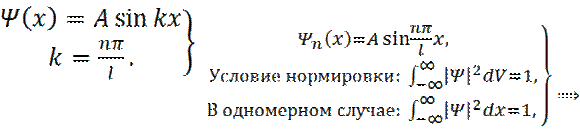
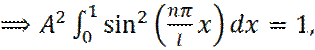 на концах промежутка интегрирования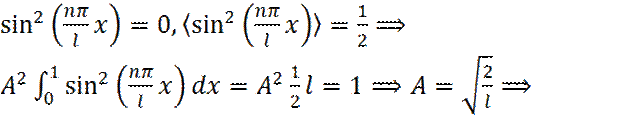

Собственным функциям 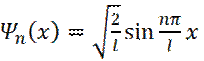соответствуют уровни энергии

3. 7. 1. Энергетический интервал между двумя соседними уровнями

3. 7. 2.  Влияние размера ямы l

Свободный электрон в металле, размер ямы  т. е. энергетические уровни расположены так тесно, что спектр можно считать непрерывным для зоны проводимости.

Размер ямы соизмерим с атомом  т. е. дискретные значения энергии, спектр – линейчатый.

3. 7. 3.  Влияние главного квантового числа n

 

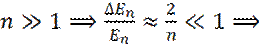 соседние уровни расположены очень тесно, можно говорить о непрерывных уровнях, т. е. о энергетической зоне (квазинепрерывные уровни).

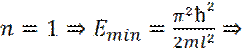частица в потенциальной яме и не может иметь энергию, меньше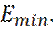

Все остальные уровни 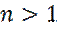 имеют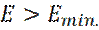

Контрольное задание 1.

    Оценить значения первых двух энергетических уровней электрона в потенциальной яме размером 1 Ǻ   

с бесконечно высокими стенками.

 

Масса электрона составляет 9, 1 10^{-31 кг.}

 

Контрольное задание 2.

    Имеется проводник со свободной квантовой частицей (электроном) длиной X.

Найти вероятность P нахождения частицы (электрона) на отрезке [0; Δ x].

 

Глава 4. ДВИЖЕНИЕ НАНОЧАСТИЦ ВО ВНЕШНЕМ ПОЛЕ

4. 1. Осцилляции частиц в параболическом внешнем поле

Этот случай интересен для описания осцилляций молекул во внешнем параболическом поле (яме).

Пусть параболическая форма внешнего поля 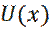 не ограничена по координате x, т. е.:

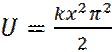   (1)

Или, для молекулы, с массой m и частотой собственных колебаний 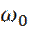 , будет:

    (2)

Тогда, уравнение Шредингера приобретает вид:

 (3)

Аналитическое решение уравнения (3) (собственные функции), находят в виде степенного ряда. Соответствующий спектр энергий 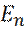 дискретен и равен:

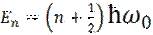   (4)

Отметим, что энергетические уровни 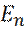 линейно зависят от n и расположены через одинаковые промежутки. Кроме того, при n = 0, существует собственное значение с ненулевой энергией (энергия нулевых колебаний):

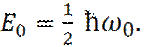(5)

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: