 |
3.3 Операторы в квантовой механике
|
|
|
|
3. 3 Операторы в квантовой механике
В квантовой механике, для каждой наблюдаемой величины частицы (импульса, энергии и т. д. ), должен быть задан оператор, переводящий волновую функцию состояния Ψ (r, t), в интересующую наблюдаемую величину.
Примеры операторов: умножение на X, f(X), дифференцирование, интегрирование и т. д.
Операторы в квантовой механике обозначаются соответствующей буквой с крышкой: Û, Ê, Â, Ĥ.
Например:
 (12)
(12)
Общее правило, позволяющее находить операторы различных физических величин, заключается в следующем: Формулы классической физики, описывающие связи между различными величинами, заменяются такими же формулами, связывающие операторы этих величин.
Например, связь между квадратом импульса и квадратами его проекций определяется в классической механике как:
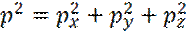 . (13)
. (13)
Соответствующий оператор квадрата импульса, имеет вид:
 (14)
(14)
Или после преобразований получаем:
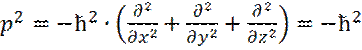 (15)
(15)
где 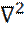 - оператор Лапласа.
- оператор Лапласа.
Аналогичным образом находим оператор кинетической энергии Ḱ :
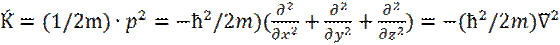 (16)
(16)
Оператор полной энергии частиц Ĥ – гамильтониан:
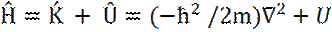 , (17)
, (17)
где U – потенциальная энергия частицы.
В классической физике, если частица движется в потенциальном поле U(x),
То ее полная энергия выражается формулой:
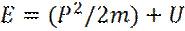 (18)
(18)
Чтобы получить волновой аналог этого соотношения необходимо заменить величины E, p2 и U соответствующими операторами и провести ряд нетривиальных преобразований. Так было открыто в 1926 году австрийским физиком Эрвином Шредингером фундаментальное уравнение квантовой механики – уравнение Шредингера.
3. 4. Уравнение Шредингера
|
|
|
Для частицы массой m, движущейся в поле с потенциальной энергией U(x, y, z, t) со скоростью v < < c, уравнение Шредингера имеет вид:
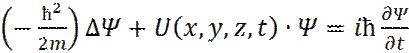 (19)
(19)
где: 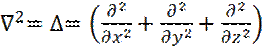 - оператор Лапласа.
- оператор Лапласа.
Уравнение Шредингера играет в квантовой механике такую же роль, как и закон Ньютона в классической механике.
Причем, Ψ –функция должна быть:
1) Конечная, непрерывная, однозначная;
2) Иметь непрерывные производные по координатам;
3) Удовлетворять условию нормировки ∫ V | Ψ |2 dV = 1.
Особую роль в квантовой механике играют стационарные состояния.
К ним относится, в частности, случай когда внешнее потенциальное поле не зависит от времени. В этом случае искомую волновую функцию можно искать в виде:
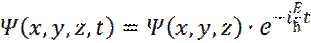 (20)
(20)
Где:
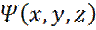 – функция координат;
– функция координат;
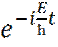 – функция t
– функция t
Получим стационарное уравнение Шредингера. Для этого подставим решение (20), в исходное уравнение Шредингера (19). Получаем:
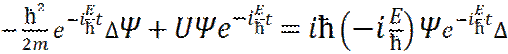 (21)
(21)
Где 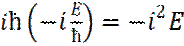
3. 5. Стационарное уравнение Шредингера
Сокращая экспоненту в левой и правой частях уравнения (21) и умножая обе части на 2m/ħ 2, получаем запись стационарного уравнения Шредингера:
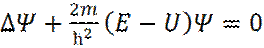 (22)
(22)
Решение этого уравнения имеет бесконечное множество решений, но с учетом условий, накладываемых на -функцию (регулярная, непрерывны первые производные, т. е. на 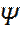 -функцию накладываются граничные условия), отбираются только решения, имеющие физический смысл – собственные функции.
-функцию накладываются граничные условия), отбираются только решения, имеющие физический смысл – собственные функции.
Собственные функции существуют лишь при определенных значениях полной энергии Е, называемых собственными значениями энергии. Совокупность собственных значений Е образуют энергетический спектр частицы.
Если потенциальная энергия U – монотонная функция и U→ 0 на бесконечности, то в области E< 0 собственные значения энергии образуют дискретный спектр.
Отыскание собственных значений энергии E и собственных -функций составляет основную задачу квантовой механики.
|
|
|
|
|
|


