 |
4.2. Прохождение частицы через потенциальный барьер
|
|
|
|
4. 2. Прохождение частицы через потенциальный барьер
4. 2. 1. Туннелирование
В этом случае, внешний потенциал  , имеет вид:
, имеет вид:
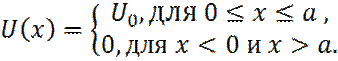 (6)
(6)
Если обозначить области до барьера, в барьере и после барьера, соответственно, I, II и III, то в областях I и III, уравнение Шредингера примет вид 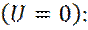
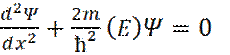 (7)
(7)
а в области II 
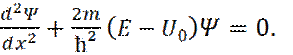 (8)
(8)
В каждой из областей, решение уравнения Шредингера имеет вид:
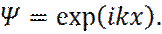 (9)
(9)
Постановка этого решения (8), в исходное уравнение (7), для областей I и III, дает связь волнового числа K, с общей энергией частицы E:
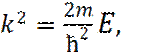 (10)
(10)
Или
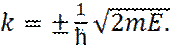 (11)
(11)
В последнем соотношении, знак «+» соответствует волне, идущей слева направо, а знак «-» - волне, идущей справа налево. Таким образом, получаем следующее решение уравнения Шредингера, в областях I и III:
 (12)
(12)
Соответственно, подстановка общего решения (9), в уравнение Шредингера, для II области (уравнение (8)), приводит к следующему характеристическому уравнению для 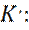
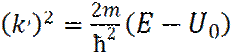 (13)
(13)
Или
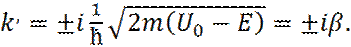 (14)
(14)
Таким образом, после подстановки 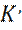 , в общее решение уравнения Шредингера (9), для области II, решение является суммой убывающей и возрастающей экспонент:
, в общее решение уравнения Шредингера (9), для области II, решение является суммой убывающей и возрастающей экспонент:
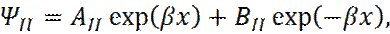 (15)
(15)
где:
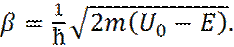 (16)
(16)
В области III, волна идет слева направо, и граничное условие при 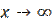 (граничное условие Зоммерфельда, определяющее единственность решения), требует, чтобы
(граничное условие Зоммерфельда, определяющее единственность решения), требует, чтобы 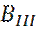 равнялось 0, в решении
равнялось 0, в решении 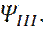
Условия сшивки решений на границе барьера имеют вид:
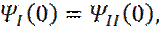 (17)
(17)
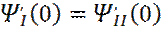 , (производные) (18)
, (производные) (18)
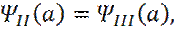 (19)
(19)
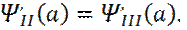 (производные) (20)
(производные) (20)
Таким образом, имеем 4 условия сшивки, и 5 неизвестных коэффициентов 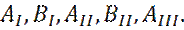 Один коэффициент получается произвольным, в силу однородности уравнения Шредингера.
Один коэффициент получается произвольным, в силу однородности уравнения Шредингера.
Тогда положим, коэффициент 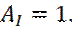 Получаем после подстановки решений
Получаем после подстановки решений 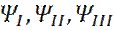 , в соотношения (17) - (20), следующее:
, в соотношения (17) - (20), следующее:
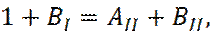 (21)
(21)
 (22)
(22)
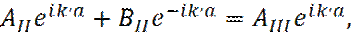 (23)
(23)
|
|
|
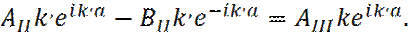 (24)
(24)
Отношение квадратов модулей амплитуд отраженной и падающей волны:
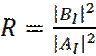 (25)
(25)
есть коэффициент отражения, и определяет вероятность отражения частицы от потенциального барьера.
Отношение квадратов модулей прошедшей и падающей волны:
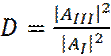 (26)
(26)
Определяет вероятность прохождения частицы через барьер.
С учетом системы уравнений (21) – (24), получаем:
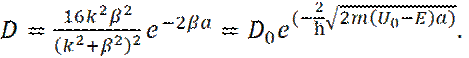 (27)
(27)
Из последнего соотношения видно, что вероятность прохождения барьера сильно повышается с уменьшением ширины барьера a, и уменьшением 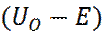 .
.
Эксоненциальная зависимость квеличения вероятности туннелирования (прохождения) частицей потенциального барьера, с уменьшением ширины барьера, использована при создании сканируюшего туннельного микроскопа, где атомно-острая игла размещается на наномеровом расстоянии от поверхности проводника, что значительно увеличивает ток туннелирования через барьер игла-проводник. В этом случае, расстояние от иглы до образца играет роль ширины барьера, и при a = 0, 5 нм, высоте барьера 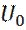 = 4 эв, создается заметный поток туннелирующих электронов, от образца к игле
= 4 эв, создается заметный поток туннелирующих электронов, от образца к игле 
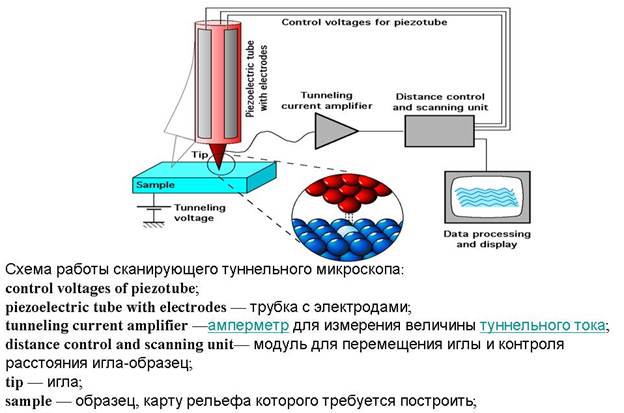




4. 3. Электрон в периодическом силовом поле. Кристаллы
Рассмотрим задачу описания состояния электрона во внешнем периодическом поле. Такое поле возникает, в частности, в кристаллах.
Уравнение Шредингера, в этом случае, записывается, как:
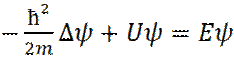 (28)
(28)
Со следующими граничными условиями периодической решетки:
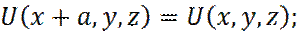 (29)
(29)
 (30)
(30)
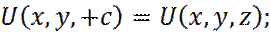 (31)
(31)
Исследованиями доказано, что решение уравнения Шредингера с периодическим потенциалом U, имеет вид:
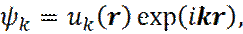 (32)
(32)
Где 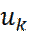 имеет период потенциала решетки.
имеет период потенциала решетки.
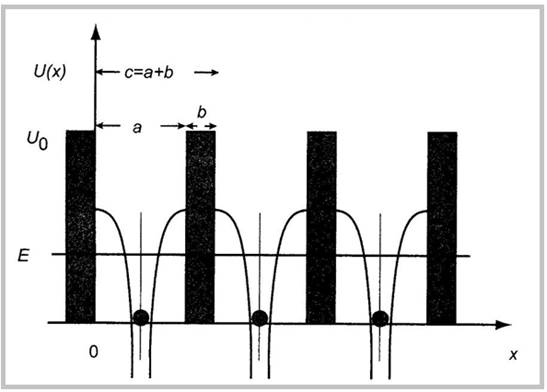
Рассмотрим частный случай (модель Кронига-Пенни), допускающий аналитическое решение. Пусть потенциал U аппроксимируется периодически повторяющимися прямоугольной ямой, шириной а, и прямоугольным барьером, шириной b.
На рисунке изображен потенциал ядер в кристалле и аппроксимирующий потенциал.
|
|
|
Для потенциальной ямы, решение уравнения Шредингера, для n-го участка, имеет вид:
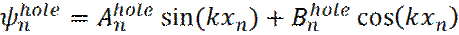 , (33)
, (33)
а для потенциального барьера:
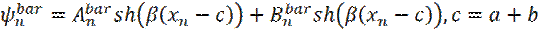 (34)
(34)
|
|
|


