Называют законом Стефана-Больцмана.

Равновесная плотность энергии излучения.

Рассмотрим излучение, находящееся в равновесии с веществом. Такое излучение будет существовать в вакууммированной полости, стенки которой поддерживаются при температуре Т. Энергия излучения распределена в объеме с определенной плотностью . Спектральное распределение энергии в полости можно охарактеризовать функцией , такой, что плотность энергии в интервале частот от до определяется соотношением:

. (31.12)

На основе законов термодинамики можно доказать, что плотность энергии излучения зависит только от температуры, и не зависит от других свойств стенок полости.

Действительно, представим себе что имеются две полости из разных материалов, но с одинаковой температурой Т. Будем рассуждать методом «от противного». Допустим, что плотности энергии в полостях неодинаковы: . Соединим полости небольшим отверстием. Поток энергии из певой полости во вторую будет больше. Это приведет к тому, что плотность энергии в первой полости уменьшится и ее стены будут больше излучать энергии, чем поглощать. Тогда стенки первой полости начнут охлаждаться. Во второй полости ситуация противоположная, и ее полости начнут нагреваться. В результате мы получим два тела, которые первоначально имели одинаковую температуру, а в результате теплообмена между ними, их температуры стали различными. Такие процессы запрещены вторым началом термодинамики, а значит исходное предположэение неверно и независимо от материала, из которго изготовлены стенки полостей.

Равновесная плотность энергии излучения внутри полости с абсолютно черными стенками связана с энергетической светимостью абсолютно черного тела . Если бы излучение с плотностью энергии представляло собой направленный поток электромагнитных волн, то вектор Пойтнинга , характеризующий плотность потока энергии волн, можно было бы найти как произведение . Однако в полости у излучения присутствуют все направления движения. Поэтому поток энергии равномерно распределен в пределах телесного угла . Соответственно, через каждую точку полости в любом направлении в пределах телесного угла распространяется поток с плотностью

. (31.13)

Площадка поверхности полости посылает в направлении перпендикуляра к ней поток энергии . В направлении, составляющем с нормалью угол , поток энергии будет равен:

(31.14)

Учтем, что и подставив выражение для в (31.14) получим:

. (31.15)

Для того, чтобы получить полный поток энергии от элемента 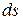по всем направлениям, другими словами в пределах телесного угла , необходимо проинтегрировать (31.15) в пределах от 0 до по углу , и в пределах от 0 до по углу :

(31.16)

С другой стороны, в соответствии с определением энергетической светимости, поток энергии, испускаемый 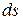, может быть представлен в виде:

(31.17)

Сравнивая (31.16) и (31.17) находим:

. (31.18)

Это соотношение должно выполнятся для каждой спектральной составляющей излучения. Поэтому для испускательной способности абсолютно черного тела должно быть справедливо:

. (31.19)

Формула Рэлея - Джинса

Расчет теоретического вида функции сыграл в истории физики чрезвычайно важную роль.

Рэлей и Джинс рассчитали равновесную плотность излучения исходя из предположения, что равновесное излучение в полости представляет собой систему стоячих волн. Согласно классической теореме о равном распределении энергии по степеням свободы, они предположили, что на каждое электромагнитное колебание приходится в среднем энергия

Можно доказать, что количество стоячих волн, с частотами в интервале от до , отнесенное к единице объема полости, равно:

. (31.20)

Поскольку электромагнитные волны поперечны, то вдоль заданного направления могут независимо распространяться две волны, поляризованные во взаимно- перпендикулярных направлениях. Поэтому в действительности

. (31.21)

Умножив на среднюю энергию колебания kT, получимплотность энергии приходящуюся на интервал частот от до

. (31.22)

. (31.23)

. (31.24)

Соответственно испускательная способность абсолютно-черного тела,

. (31.25)

Однако эта функция совпадает с экспериментальными данными только при больших длинах волн. Это видно на рисунке 31.7, где показан примерный вид экспериментальной и теоретической зависимостей (если в (31.25) перейти к зависимости от длины волны). Вполне очевидно, что при интегрировании во всем диапазоне частот, т.е. при вычислении , получим бесконечное значение. Это очевидное противоречие теоретического результата и эксперимента получило название ультрафиолетовой катастрофы. Это связано с тем, что рассуждения Рэлея и Джинса основывались на фундаментальных законах классической физики. Логически рассуждения, приводящие к формуле (31.25), абсолютно безупречны, что указывало необходимость внесения корректировок в фундаментальные представления, существование некоторых иных, неклассических закономерностей.

Формула Планка

Выход из состояния «ультрафиолетовой катастрофы» был найден М. Планком, который получил формулу, верно описывающую испускательную способность абсолютно черного тела, предположив, что электромагнитная энергия излучается квантами, т.е. отдельными дискретными порциями. Это приводит к тому, что средняя энергия колебания оказывается не равна .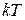

Энергия каждого кванта определяется соотношением

. (31.26)

где , называется постоянной Планка и является фундаментальной физической константой.

Если излучение испускается квантами 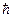w, то его энергия должна быть кратна этой величине:

. (31.27)

В состоянии равновесия распределение колебаний по значениям энергии описывается распределением Больцмана, в соответствии с которым: если имеется объектов, энергия которых может принимать значения из ряда возможных , то количество объектов в состоянии с определяется выражением

. (29.28)

В нашем случае вероятность того, что энергия колебания частоты w равна ,определя­ется выражением:

. (31.29)

где: - количество колебаний с энергией

-общее количество колебаний.

Среднее значение энергии колебания

. (31.30)

. (31.31)

Обозначим . Тогда выражение для средней энергии колебания можно представить в виде:

. (31.32)

Действительно, по правилам дифференцирования:

,

то есть

Но сумма есть сумма членов геометрической прогрессии с первым чле­ном b₁ = 1 и знаменателем . Из элементарной математики известна формула для суммы членов геометрической прогрессии

. (31.33)

Подставив и b₁ = 1, находим:

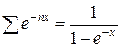. (31.34)

Это значение для суммы подставим в (31.32) и выполним дифференцирование:

. (31.35)

Подставив , получим

. (31.36)

Итак, средняя энергия колебания оказывается равной

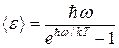. (31.37)

Важно отметить, что если мысленно устремить постоянную Планка к нулю – –, то есть предположить что энергия излучения изменяется не дискретно, а непрерывно, то по формулам приближенных вычислений получаем:

и .

Таким образом, если бы энергия излучения могла бы принимать непрерыв­ный ряд значений ее среднее значение было бы kT.

Умножив на количество колебаний в интервале от до , найдем энер­гию приходящуюся на интервал частот :

. (31.38)

Значит

. (31.39)

Воспользовавшись соотношением (31.19) найдем

. (31.40)

Эта формула точно согласуется с экспериментальными данными. Для энергетической светимости абсолютно черного тела получается в этом случае

Вычисления дают:

,

т.е. постоянная Стефана-Больцмана

что очень хорошо согласуется с экспериментом.

Формула (31.40) позволяет объяснить и закон смещения Вина. Таким образом (31.40) дает верное и исчерпывающее описание равновесного теплового излучения. Но, напомним, для ее получения пришлось предположить, что излучение испускается отдельными квантами с энергией

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: