 |
Принцип неопределенности Гейзенберга.
|
|
|
|
В квантовой механике состояние частицы определяется заданием значений координат, импульса, энергии и других подобных величин, которые называются динамическими переменными.
Строго говоря, микрообъекту не могут быть приписаны динамические переменные. Однако информацию о микрообъекте мы 
получаем в результате их взаимодействия с макроприборами. Поэтому необходимо результаты измерений выражаются в динамических переменных. Поэтому, например, говорят о состоянии электрона с определенной энергией.
Своеобразие свойств микрообъектов заключается в том, что не для всех переменных получаются при изменениях определенные значения. Так в мысленном эксперименте мы видели, что при попытке уменьшить неопределенность координаты электронов в пучке путем уменьшения ширины щели приводит к появлению у них неопределенной составляющей импульса в направлении соответствующей координаты. Между неопределенностями координаты 
и импульса 
имеет место соотношение
(33.4)
Аналогичное соотношение имеет место для других осей координат и соответствующих проекций импульса, а также для ряда других пар величин. В квантовой механике такие пары величин называются 
канонически сопряженными. Обозначив канонически сопряженными величины А и В, можно записать:
(33.5)
Соотношение (33.5) было установлено в 1927 году Гейзенбергом и называется соотношением неопределенности.
Само утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше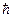 
принципом неопределенности Гейзенберга. Принцип неопределенности Гейзенберга является одним из фундаментальных положений квантовой механики.
|
|
|
Важно отметить, что канонически сопряженными являются энергия и время, и справедливо соотношение:
(33.6)
(33.6) в частности, означает, что для измерения энергии с погрешностью не более (порядка) 
необходимо затратить время не менее 
. С другой стороны, если известно, что в некотором состоянии частица не может находиться более 
, то можно утверждать что энергия частицы в этом состоянии не может быть определена с погрешностью менее 
Соотношение неопределенностей определяет возможность использования классических понятий для описания микрообъектов. Очевидно, что чем больше масса частицы, тем меньше произведение неопределенностей ее координаты и скорости 
. Для частиц с размерами порядка микрометра неопределенности координаты и скорости становятся столь малы, что оказываются за пределами точности измерений, и движение таких частиц можно рассматривать происходящим по определенной траектории.
При определённых условиях даже движение микрочастицы может рассматриваться, как происходящее по траектории. Например, движение электрона в ЭЛТ.
Соотношение неопределенностей, в частности, позволяет объяснить, почему электрон в атоме не падает на ядро. При падении электрона на ядро его координаты и импульс приняли бы одновременно определенные, а именно нулевые значения, что запрещено принципом неопределенности. Важно отметить, что принцип неопределенности – это базовое положение, которое определяет невозможность падения электрона на ядро наряду с рядом других следствий без принятия дополнительных постулатов.
Оценим на основе соотношения неопределенностей минимальные размеры атома водорода. Формально, с классической точки зрения, энергия должна быть минимальна при падении электрона на ядро, т.е. пр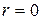и 
и 
. Поэтому для оценки минимальной размеров атома водорода можно считать что, что его координата и импульс совпадают с неопределенностями этих величин: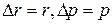 
. Тогда они должны быть связаны соотношением:
|
|
|
(33.7)
Энергия электрона в атоме водорода выражается формулой:
(33.8)
Выразим импульс из (33.7) и подставим в (33.8):
. (33.9)
Найдем радиус орбиты 
, при котором энергия минимальна. Дифференцируя (33.9) и приравнивая производную нулю, получаем:
. (33.10)
Поэтому радиус расстояние от ядра, на котором электрон имеет минимальную энергию в атоме водорода, можно оценить по соотношению
. (33.11)
Это значение совпадает с радиусом воровской орбиты.
Подставив найденное расстояние в формулу (33.9), получим выражение для минимальной энергии электрона в атоме водорода:
. (33.12)
Это выражение также совпадает с энергией электрона на орбите минимального радиуса в теории Бора.
Уравнение Шрёдингера
Поскольку, по идее Де-Бройля, движение микрочастицы связано с некоторым волновым процессом, Шрёдингер сопоставил ее движению комплексную функцию координат и времени, которую он назвал волновой функцией и обозначил 
. Часто это функцию так и называют – «пси-функция». В 1926 году Шрёдингер сформулировал уравнение, которому должна удовлетворять 
:
. (33.13)
В этом уравнении:
m – масса частицы;
;
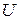– функция координат и времени, градиент, который с обратным знаком определяет силу, действующую на частицу.
Уравнение (33.13) называется уравнением Шрёдингера. Отметим, что уравнение Шрёдингера не выводится из каких-либо дополнительных соображений. Фактически оно является постулатом квантовой механики, сформулированным на основе аналогии уравнений оптики и аналитической механики. Фактическим обоснованием уравнения (33.13) Является соответствие результатов, полученных на его основе экспериментальным фактам.
Решая (33.13), получают вид волновой функции, описывающей рассматриваемую физическую систему, например, состояния электронов в атомах. Конкретный вид - функции определяется характером силового поля, в котором находится частица, т.е. функцией .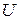
Если силовое поле стационарно, то 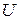не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шрёдингера распадается на два множителя, один из которых зависит только от координат, другой – только от времени:
. (33.14)
|
|
|
где 
– полная энергия системы, которая в случае стационарного поля остаётся постоянной.
Подставив (33.14) в (33.13), получим:
После сокращения на ненулевой множитель 
получаем уравнение Шредингера, справедливое в указанных ограничениях:
. (33.15)
Уравнение (33.15) называется уравнением Шрёдингера для стационарных состояний, которое обычно записывают в виде:
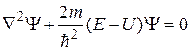. (33.16)
В квантовой механике широко используется понятие оператора. Под оператором подразумевают символ, указывающий правило, посредством которого одной функции, 
, сопоставляется другая – f:
. (33.17)
(Оператором можно считать набор символов, например, sin(), который подразумевает действия, которые необходимо совершить, чтобы рассчитать синус выражения в скобках. Так оператор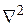 
означает, что необходимо найти сумму вторых частных производных по координатам.)
Обозначим
. (33.18)
Оператор 
называется оператором Гамильтона (гамильтонианом)
Воспользовавшись этим обозначением, уравнению (33.15) можно придать вид:
. (33.19)
Решение уравнения (33.18) позволяет найти возможные значения параметра и вид волновых функций, соответствующих им. Параметр в (33.18) имеет смысл энергии рассматриваемой системы. Допустимые значения параметра соответствуют возможным значениям энергии системы (собственным значениям). Поэтому говорят, что оператор Гамильтона является оператором энергии. А уравнения Шрёдингера вида (33.18) называют уравнениями Шредингера для собственных значений.
В квантовой механике каждой физической величине (динамической переменной) 
сопоставляется оператор, который обычно обозначают соответствующей прописной буквой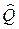 
. Например, операторы координат, импульса, момента импульса и т. д. С использованием каждого оператора можно записать уравнение, аналогичное по виду (33.18). Решая такие уравнения (т.е. уравнения типа (33.18) 
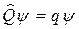), находят собственные значения 
.
|
|
|
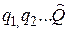