 |
Тормозное рентгеновское излучение
|
|
|
|
 Представление о испускании излучения квантами величиной
Представление о испускании излучения квантами величиной 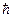 w, оказалось эффективным для объяснения свойств теплового излучения. Однако прямое экспериментальное подтверждение этого способа излучения было получено при исследовании спектра тормозного рентгеновского излучения.
w, оказалось эффективным для объяснения свойств теплового излучения. Однако прямое экспериментальное подтверждение этого способа излучения было получено при исследовании спектра тормозного рентгеновского излучения.
В рентгеновской трубке электроны, вылетевшие из катода в результате термоэлектронной эмиссии, ускоряются анодным напряжением и попадают в твердый тугоплавкий анод. Быстрое торможение электронов в аноде означает движение с большим ускорением, которое сопровождается излучением электромагнитных волн в широком диапазоне частот.
По представлениям классической электродинамики должны излучаться все длины волн. 
 Длина волны, на которую приходится максимум мощности излучения, должна уменьшаться по мере увеличения скорости электронов. Экспериментально такая зависимость действительно наблюдается – рисунок 31.9. Т.е. теория под
Длина волны, на которую приходится максимум мощности излучения, должна уменьшаться по мере увеличения скорости электронов. Экспериментально такая зависимость действительно наблюдается – рисунок 31.9. Т.е. теория под  тверждается, но имеется принципиальное отличие: кривые не идут к началу координат (!).
тверждается, но имеется принципиальное отличие: кривые не идут к началу координат (!).
С квантовой точки зрения это легко объясняется. Величина энергии кванта электромагнитного излучения не может превысить энергию электрона, полученную им при движении в электрическом поле между анодом и катодом  .
.
Следовательно,
 . (31.41)
. (31.41)
Найденное из (31.41) значение 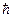 хорошо согласуется со значениями, определенными иными способами. Мало того этот способ нахождения
хорошо согласуется со значениями, определенными иными способами. Мало того этот способ нахождения 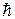 считается ныне самым точным.
считается ныне самым точным.
Фотоэффект.
В 1887 г. Г. Герц заметил, что проскакивание искры между электродами значительно облегчается, если один из шариков осветить ультрафиолетовыми лучами. Так был открыт фотоэффект.
 | |||
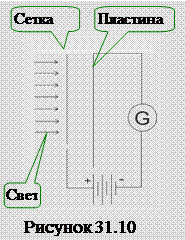 | |||
В 1888 г. – 1889 г. фотоэффект тщательно изучался Столетовым на приборе, показанном схематически на рисунке 31.10.
|
|
|
Конденсатор, образованный проволочной сеткой и сплошной пластиной включался последовательно с гальванометром и источником тока. Сплошная пластина освещается через сетку светом, а в цепи регистрируется фототок. Столетов установил, что:
1. Наибольшее действие указывают ультрафиолетовые лучи.
2. Сила тока возрастает с увеличением освещённости.
3. Испускаемые катодом частицы имеют отрицательный заряд.
Впоследствии было установлено, что испускаемые частицы являются электронами.
 В настоящее время фотоэффект можно изучать на установке, схематически показанной на рисунке 31.11. Полученная на таком приборе вольтамперная характеристика, т. е. Зависимость анодного тока
В настоящее время фотоэффект можно изучать на установке, схематически показанной на рисунке 31.11. Полученная на таком приборе вольтамперная характеристика, т. е. Зависимость анодного тока 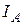 от напряжения
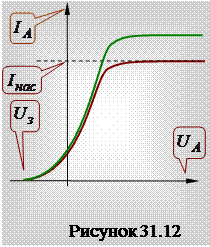
от напряжения  , имеет вид, показанный приблизительно на рисунке 31.12.
, имеет вид, показанный приблизительно на рисунке 31.12.
Основными особенностями этой кривой, снимаемой при постоянном световом потоке, является наличие тока насыщения и ненулевой ток при нулевом анодном напряжении  = 0. Пологий ход кривой указывает на то, что электроны вылетают с различными по величине скоростями. Для обращения силы тока в нуль необходимо приложить задерживающее напряжение
= 0. Пологий ход кривой указывает на то, что электроны вылетают с различными по величине скоростями. Для обращения силы тока в нуль необходимо приложить задерживающее напряжение  , при котором даже самые быстрые электроны со скоростями
, при котором даже самые быстрые электроны со скоростями  не долетают до анода. Поэтому
не долетают до анода. Поэтому
 , (31.42)
, (31.42)
Основные экспериментальные факты, полученные при изучении фотоэффекта, сводятся к следующему:
1 При постоянном спектральном составе излучения, фототок насыщения пропорционален световому потоку, что называют законом Столетова.
2 Максимальная скоростьфотоэлектронов  не зависит от интенсивности света, но зависит от спектрального состава излучения.
не зависит от интенсивности света, но зависит от спектрального состава излучения.
3 Для каждого вещества существует такая длина волны 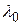 , что если длина волны излучения
, что если длина волны излучения 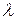 >
> 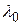 , то фотоэффект отсутствует. Длину волны
, то фотоэффект отсутствует. Длину волны 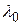 называют красной границей фотоэффекта.
называют красной границей фотоэффекта.
Иногда можно слышать утверждение о том, что «фотоэффект не объясняется классической волновой теорией световых явлений». В действительности ситуация состоит в том, что существование фотоэффекта вполне соответствует волновым представлениям – при большой амплитуде вынужденных колебаний электронов они могут вылетать с поверхности металла и создавать фототок. Закон Столетова (пропорциональность фототока насыщения световому потоку) также не противоречит волновым представлениям – с ростом интенсивности света увеличивается доля электронов, способных вылететь за пределы металла.
|
|
|
Однако в рамках волновой теории непонятна независимость  , от интенсивности падающего света. Амплитудой вынужденных колебаний пропорциональна амплитуде волны. Скорость вылетающих электронов должна зависеть от интенсивности падающего света, чего в эксперименте не наблюдается. Необъяснимы также зависимость максимальной скорости от спектрального состава излучения и существование красной границы фотоэффекта.
, от интенсивности падающего света. Амплитудой вынужденных колебаний пропорциональна амплитуде волны. Скорость вылетающих электронов должна зависеть от интенсивности падающего света, чего в эксперименте не наблюдается. Необъяснимы также зависимость максимальной скорости от спектрального состава излучения и существование красной границы фотоэффекта.
В 1905г. Эйнштейн показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет не только испускается квантами  , но и поглощается такими же квантами. При этом вся энергия кванта
, но и поглощается такими же квантами. При этом вся энергия кванта  полностью «усваивается» электроном. Часть этой энергии затрачивается на преодоление работы выхода
полностью «усваивается» электроном. Часть этой энергии затрачивается на преодоление работы выхода  , а остаток идет на сообщение электрону кинетической энергии. Работой выхода называется наименьшая энергия, необходимая для удаления, электрона из тела в вакуум. Подробней природу работы выхода рассмотрим позднее.
, а остаток идет на сообщение электрону кинетической энергии. Работой выхода называется наименьшая энергия, необходимая для удаления, электрона из тела в вакуум. Подробней природу работы выхода рассмотрим позднее.
Исходя из этих предположений, Эйнштейн написал уравнение
 , (31.43)
, (31.43)
которое называют уравнением Эйнштейна для фотоэффекта.
Из (31.43) вытекает, что если 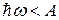 , то фотоэффект не наблюдается. Этим объясняется существование красной границы фотоэффекта.
, то фотоэффект не наблюдается. Этим объясняется существование красной границы фотоэффекта.
В соответствии с (31.43)
 .
.
И это объясняет зависимость  от спектрального состава излучения.
от спектрального состава излучения.
Если 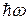 > А, то фотоэлектроны за счет кинетической энергии способны долететь до анода, чем объясняется ненулевой фототок при нулевом
> А, то фотоэлектроны за счет кинетической энергии способны долететь до анода, чем объясняется ненулевой фототок при нулевом  .
.
Число фотоэлектронов пропорционально числу падающих на катод квантов, которое в свою очередь пропорционально световому потоку. При протекании тока насыщения все вырванные электроны участвуют в создании тока. Соответственно ток насыщения должен быть пропорционален световому потоку, чем объясняется закон Столетова.
|
|
|
Опыт Боте. Фотоны
Итак, чтобы объяснить распределение энергии в спектре равновесного теплового излучения пришлось предположить, что свет испускается квантами 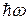 .
.
 Для объяснения фотоэффекта необходимо предположить, что свет поглощается квантами. Эйнштейн выдвинул гипотезу о том, что свет распространяется также в виде дискретных частиц световых квантов, которые позднее стали называться фотонами. Для непосредственной проверки гипотезы Эйнштейна Боте поставил специальный эксперимент, идея которого заключалась в том, что при очень низкой интенсивности излучения фотоны должны излучаться и распространяться отдельными объектами, которые можно зарегистрировать. Схема экспериментальной установки Боте показана на рисунке 31.13.
Для объяснения фотоэффекта необходимо предположить, что свет поглощается квантами. Эйнштейн выдвинул гипотезу о том, что свет распространяется также в виде дискретных частиц световых квантов, которые позднее стали называться фотонами. Для непосредственной проверки гипотезы Эйнштейна Боте поставил специальный эксперимент, идея которого заключалась в том, что при очень низкой интенсивности излучения фотоны должны излучаться и распространяться отдельными объектами, которые можно зарегистрировать. Схема экспериментальной установки Боте показана на рисунке 31.13.
Металлическая фольга освещалась через диафрагму слабым пучком рентгеновских лучей. При этом она сама становилась источником рентгеновского излучения очень низкой интенсивности, так что можно было считать, что от фольги распространяются отдельные фотоны. С обеих сторон от фольги помещались газоразрядные счетчики. Счетчики были соединены с механизмами, так что при срабатывании счетчика на движущейся между счетчиками ленте ставилась метка.
Если энергия, излучаемая фольгой в виде рентгеновских лучей, распространяется во все стороны равномерно, в соответствии с волновыми представлениями, то следовало ожидать одновременного срабатывание счетчиков. Если же от фольги летят отдельные фотоны, каждый в своем направлении, то счетчики должны срабатывать беспорядочно. В первом случае метки на ленте должны располагаться попарно, во втором беспорядочно.
В эксперименте счетчики срабатывали совершенно беспорядочно, что экспериментально доказало испускание света отдельными фотонами.
Фотон характеризуется его энергией, которая имеет значение:
 , (31.44)
, (31.44)
Согласно теории относительности, частица с энергией  обладает реляти вистской массой
обладает реляти вистской массой
 , (31.45)
, (31.45)
|
|
|
Фотон движется со скоростью света в вакууме с. Поскольку 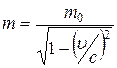 , и подстановка
, и подстановка  обращает корень в нуль, масса покоя фотона равна нулю:
обращает корень в нуль, масса покоя фотона равна нулю:
 (31.46)
(31.46)
Следовательно, фотон особая частица, отличающаяся от других, отсутствием массы покоя.
Согласно теории относительности, энергия частицы может быть представлена в виде
 , (31.47)
, (31.47)
где p – импульс частицы.
Соответственно импульс фотона ( ):
):
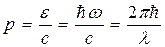 , (31.48)
, (31.48)
Учитывая, что  есть волновое число, направление движения фотона совпадает с направлением распространения световой волны и его импульс и волновой вектор волны совпадают по направлению, для импульса фотона можно записать соотношение:
есть волновое число, направление движения фотона совпадает с направлением распространения световой волны и его импульс и волновой вектор волны совпадают по направлению, для импульса фотона можно записать соотношение:
 . (31.49)
. (31.49)
Итак, существует ряд явлений, которые могут быть объяснены только исходя из представлений о свете как о потоке фотонов. В то же время интерференция, дифракция могут быть объяснены только на основе волновых представлений. Следовательно, для света характерен корпускулярно-волновой дуализм, когда в одних явлениях свет ведет себя как поток частиц, а в других – как волна. (Отметим, что такой дуализм присущ и частицам вещества – электронам, протоном, атомам, молекулам.)
Согласно волновым представлениям освещенность поверхности пропорциональна квадрату амплитуды световой волны  . С корпускулярной точки зрения – плотности потока фотонов. Следовательно, плотность потока должна быть ~
. С корпускулярной точки зрения – плотности потока фотонов. Следовательно, плотность потока должна быть ~  . Можно считать, что носителем энергии и импульса является фотон, и энергия выделяется в той точке поверхности, в которую попадает фотон. А величина
. Можно считать, что носителем энергии и импульса является фотон, и энергия выделяется в той точке поверхности, в которую попадает фотон. А величина  определяет вероятность
определяет вероятность 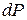 попадания в объем
попадания в объем  в окрестности данной точки:
в окрестности данной точки:
 , (31.50)
, (31.50)
Таким образом, освещенность носит статический характер, равномерность освещенности определяется тем, что при нормальной освещенности на 1  поверхности падает 2
поверхности падает 2  фотонов в секунду. Поскольку относительная флуктуация обратно пропорциональна корню из числа частиц, поверхность выглядит освещенной равномерно.
фотонов в секунду. Поскольку относительная флуктуация обратно пропорциональна корню из числа частиц, поверхность выглядит освещенной равномерно.
ЭФФЕКТ КОМПТОНА.
 Очень ярко корпускулярная природа света проявилась в эффекте Комптона, который был обнаружен в 1923 году. Исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны
Очень ярко корпускулярная природа света проявилась в эффекте Комптона, который был обнаружен в 1923 году. Исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны  присутствует излучение с
присутствует излучение с  . Причем, как было установлено экспериментально, разность длин волн рассеянного и исходного излучений
. Причем, как было установлено экспериментально, разность длин волн рассеянного и исходного излучений 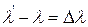 зависит только от угла
зависит только от угла  между направлением первичного пучка и направлением рассеянного излучения. От длины волны и от природы рассеивающего вещества
между направлением первичного пучка и направлением рассеянного излучения. От длины волны и от природы рассеивающего вещества 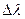 не зависит.
не зависит.
Схема эксперимента Комптона показана на рисунке. Использовалось монохроматическое рентгеновское излучение из которого диафрагмами выделялся узконаправленный пучок и направлялся на рассеивающее вещество. Регистрирующее устройство (рентгеновский спектрометр) выделяет из рассеянного излучения лучи, идущие под углом  к первоначальному направлению распространения и определяет их длину волны.
к первоначальному направлению распространения и определяет их длину волны.
|
|
|
В результате исследований Комптона были выделены две характерные особенности рассеянного излучения:
1. изменение длины  рассеянных лучей от угла рассеяния описывалось эмпирической (т.е. полученной на основе анализа экспериментальных данных) зависимостью:
рассеянных лучей от угла рассеяния описывалось эмпирической (т.е. полученной на основе анализа экспериментальных данных) зависимостью:
 , (31.51)
, (31.51)
где  - некоторая константа.
- некоторая константа.
Примерный вид графиков зависимости интенсивности рассеянного излучения от длины волны показан на рисунке 31.15.
2. 
Хотя изменение длины волны  не зависело от природы рассеивающего вещества, соотношение в рассеянном излучении интенсивностей волн с
не зависело от природы рассеивающего вещества, соотношение в рассеянном излучении интенсивностей волн с 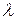 и
и  весьма сильно зависло от атомного номера рассеивающего вещества. Соответствующие зависимости для нескольких веществ показаны на рисунке 31.16
весьма сильно зависло от атомного номера рассеивающего вещества. Соответствующие зависимости для нескольких веществ показаны на рисунке 31.16

Рассеяние электромагнитных волн по классическим волновым представлениям является результатом дифракции на мелких неоднородностях. Появление в рассеянном излучении волн с большей длиной волны (как и с меньшей) представляется невозможным. (Появление в спектре дифракционной решетки волн с различной длиной является следствием использования белого света, который разлагается решеткой в спектр.) Поэтому объяснить эффект Комптона на основе волновых представлений не удалось.
Рассматривая рентгеновское излучение как поток фотонов можно предположить, что при столкновении фотонов с частицами в составе молекул вещества они могут передавать им часть своей энергии, что означает уменьшение частоты фотонов, а с точки зрения волновых представлений – соответствующее увеличение длины волны излучения.
Независимость  от природы рассеивающего вещества указывала на то, что столкновения фотонов происходят с одинаковыми во всех веществах частицами, находящимися в сходных состояниях. Такими частицами могли быть валентные электроны. Действительно, связь с ядром валентных электронов намного меньше, чем электронов внутренних оболочек атомов. По сравнению с энергией рентгеновских фотонов энергия связи валентных электронов невелика, поэтому валентные электроны различных атомов можно, в первом приближении, рассматривать как почти свободные.
от природы рассеивающего вещества указывала на то, что столкновения фотонов происходят с одинаковыми во всех веществах частицами, находящимися в сходных состояниях. Такими частицами могли быть валентные электроны. Действительно, связь с ядром валентных электронов намного меньше, чем электронов внутренних оболочек атомов. По сравнению с энергией рентгеновских фотонов энергия связи валентных электронов невелика, поэтому валентные электроны различных атомов можно, в первом приближении, рассматривать как почти свободные.
Приняв это предположение, можем достаточно просто объяснить изменение интенсивности рассеянного излучения с длиной волны 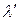 при увеличением атомного номера рассеивающего вещества. Относительная доля валентных электронов в тяжелых атомах намного меньше. При столкновении фотонов с электронами заполненных оболочек, сильно связанных с ядром, взаимодействие происходит с атомом в целом. Энергия, которую фотон передаёт в этом случае, невелика, и заметного изменения частоты фотона не происходит. Подобными столкновениями и обусловлено наличие в спектре рассеянного излучения фотонов с частотой, практически совпадающей с частотой падающего излучения. При использовании в качестве рассеивающего вещества атомов тяжелых элементов именно такие столкновения преобладают, поскольку валентных электронов относительно немного.
при увеличением атомного номера рассеивающего вещества. Относительная доля валентных электронов в тяжелых атомах намного меньше. При столкновении фотонов с электронами заполненных оболочек, сильно связанных с ядром, взаимодействие происходит с атомом в целом. Энергия, которую фотон передаёт в этом случае, невелика, и заметного изменения частоты фотона не происходит. Подобными столкновениями и обусловлено наличие в спектре рассеянного излучения фотонов с частотой, практически совпадающей с частотой падающего излучения. При использовании в качестве рассеивающего вещества атомов тяжелых элементов именно такие столкновения преобладают, поскольку валентных электронов относительно немного.
 Для объяснения зависимости
Для объяснения зависимости  рассмотрим процесс упругого столкновения фотона с почти свободными электронами. Свободными можно считать все электроны, энергия связи которых значительно меньше энергии, которую фотон может передать при столкновении.
рассмотрим процесс упругого столкновения фотона с почти свободными электронами. Свободными можно считать все электроны, энергия связи которых значительно меньше энергии, которую фотон может передать при столкновении.
Допустим, что на первоначально покоящийся свободный электрон падает фотон с энергией 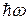 и импульсом
и импульсом  . Энергия электрона до сталкивания
. Энергия электрона до сталкивания  , импульс равный нулю.
, импульс равный нулю.
После столкновения электрон будет обладать энергией  и импульсом
и импульсом  . Под массой электрона понимаем его релятивистскую массу
. Под массой электрона понимаем его релятивистскую массу  . Энергия фотона станет
. Энергия фотона станет  . Из закона сохранения энергии следует соотношение:
. Из закона сохранения энергии следует соотношение:
 , (31.52)
, (31.52)
Из закона сохранения импульса:
 , (31.53)
, (31.53)
Разделим (8) на скорость света в вакууме с и учтём, что  :
:
 , (31.54)
, (31.54)
Выразим  :
:
 , (31.55)
, (31.55)
и возведем полученное соотношение в квадрат:
 . (31.56)
. (31.56)
По теореме косинусов из рисунка найдём:
 . (31.57)
. (31.57)
Вычитая (31.56) и (31.56), находим:
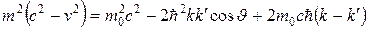 . (31.58)
. (31.58)
Из определения релятивистской массы следует:
 (31.59)
(31.59)
Учитывая (31.59), из (31.58) получаем:
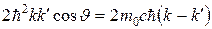 , (31.60)
, (31.60)
или
 . (31.61)
. (31.61)
Умножим (31.61) на дробь  :
:
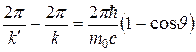 . (31.62)
. (31.62)
Учитывая, что  , находим
, находим
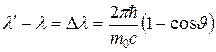 . (31.63)
. (31.63)
Это выражение совпадает с (31.51), если положить
 . (31.64)
. (31.64)
 называется комптоновской длиной волны той частицы, масса которой имеется в виду. В нашем рассмотрении это электроны.
называется комптоновской длиной волны той частицы, масса которой имеется в виду. В нашем рассмотрении это электроны.
Таким образом, на основе корпускулярных, квантовых представлений объясняются все особенности рассеяния рентгеновского излучения в веществе.
|
|
|


