 |
Проверка гипотезы о существовании тренда
|
|
|
|
Прежде чем перейти к определению тенденции и выделению тренда, нужно выяснить, существует ли вообще тенденция в исследуемом процессе. Основные подходы к решению этой задачи основаны на статистической проверке гипотез о случайности ряда: 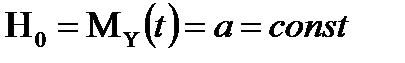 .
.
Рассмотрим один из самых простых методов, позволяющий обнаружить тренд в значении средней и дисперсии уровней. Метод разработан Ф. Фостером и А. Стюартом[4], которые предложили по данным исследуемого ряда определять величины 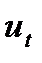 и
и 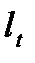 . Значения
. Значения 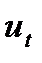 и
и 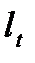 находятся путем последовательного сравнения уровней. Если какой-нибудь уровень ряда превышает по своей величине каждый из предыдущих уровней, то величине
находятся путем последовательного сравнения уровней. Если какой-нибудь уровень ряда превышает по своей величине каждый из предыдущих уровней, то величине 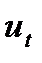 присваивается значение 1, в остальных случаях 0. Таким образом,
присваивается значение 1, в остальных случаях 0. Таким образом,
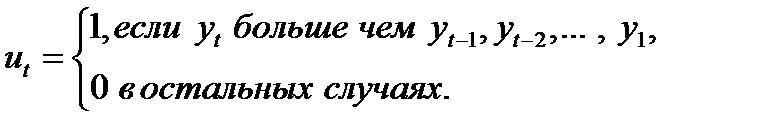 (2.1)
(2.1)
Наоборот, если уровень меньше всех предыдущих, то 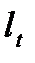 присваивается значение 1. Таким образом,
присваивается значение 1. Таким образом,
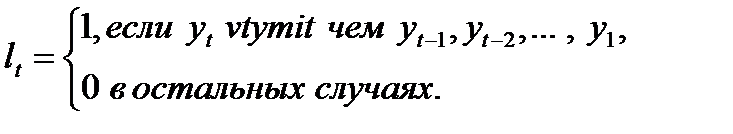 (2.2)
(2.2)
После того как 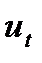 и
и 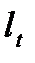 найдены, легко определить две простые характеристики
найдены, легко определить две простые характеристики 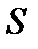 и
и 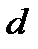 :
:
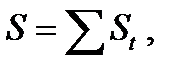 (2.3)
(2.3)
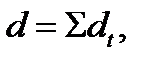 (2.4)
(2.4)
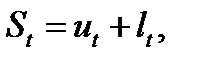 (2.5)
(2.5)
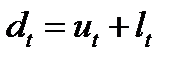 (2.6)
(2.6)
Суммирование в формулах (1.24) и (1.25) производится по всем членам ряда. Нетрудно найти, что  принимает значения 0 и 1:
принимает значения 0 и 1:  в случае, если
в случае, если  не является ни наибольшим, ни наименьшим уровнем всех предшествующих уровней, в противном случае
не является ни наибольшим, ни наименьшим уровнем всех предшествующих уровней, в противном случае 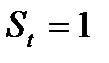 . Легко определить, что
. Легко определить, что  может находиться в пределах
может находиться в пределах 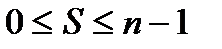 . (Здесь, как и выше,
. (Здесь, как и выше, 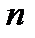 означает число членов ряда). Если все уровни равны (нулевая дисперсия), то
означает число членов ряда). Если все уровни равны (нулевая дисперсия), то 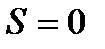 , если же они монотонно растут, или падают, или колебания их чередуются, систематически увеличиваясь или падая, то
, если же они монотонно растут, или падают, или колебания их чередуются, систематически увеличиваясь или падая, то 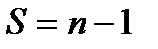 .
.
В свою очередь величина 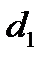 принимает значения 0; 1 и -1. Найдем теперь пределы для
принимает значения 0; 1 и -1. Найдем теперь пределы для 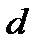 : нижний предел равен
: нижний предел равен  , верхний составляет
, верхний составляет 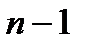 . Нижний предел соответствует монотонно убывающему, а верхний – монотонно растущему ряду. Авторы данных характеристик не рассматривают условий, когда значение
. Нижний предел соответствует монотонно убывающему, а верхний – монотонно растущему ряду. Авторы данных характеристик не рассматривают условий, когда значение 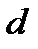
|
|
|
равно 0. Между тем именно здесь и кроется известная слабость рассматриваемого метода. В самом деле, если все уровни равны, то 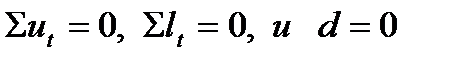 . Кроме того,
. Кроме того, 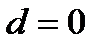 и тогда, когда
и тогда, когда  . Что касается первой ситуации, то она соответствует полному отсутствию тренда. Вторая же может наблюдаться и тогда, когда ряд охватывает два периода с противоположными тенденциями. Кроме того,
. Что касается первой ситуации, то она соответствует полному отсутствию тренда. Вторая же может наблюдаться и тогда, когда ряд охватывает два периода с противоположными тенденциями. Кроме того,  и в случае, когда подъемы и падения уровней чередуются. Если уровни симметрично располагаются вокруг горизонтальной линии, то величина
и в случае, когда подъемы и падения уровней чередуются. Если уровни симметрично располагаются вокруг горизонтальной линии, то величина 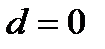 , действительно, соответствует отсутствию тренда в средней. Однако при определении
, действительно, соответствует отсутствию тренда в средней. Однако при определении 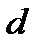 не принимаются во внимание величины отклонений от горизонтальной линии. Поэтому мыслима такая ситуация, при которой отклонения с одним знаком будут систематически выше отклонений с другим знаком. В этом случае тенденция средней к росту (падению) не отразится на величине
не принимаются во внимание величины отклонений от горизонтальной линии. Поэтому мыслима такая ситуация, при которой отклонения с одним знаком будут систематически выше отклонений с другим знаком. В этом случае тенденция средней к росту (падению) не отразится на величине 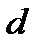 . В чистом виде такое расположение уровней будет встречаться в практике крайне редко, но надо иметь в виду, что все же оно возможно[5].
. В чистом виде такое расположение уровней будет встречаться в практике крайне редко, но надо иметь в виду, что все же оно возможно[5].
Показатели 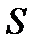 и
и 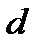 асимптотически нормальны и имеют независимые распределения. Они существенно зависят от порядка расположения уровней во времени. Показатель
асимптотически нормальны и имеют независимые распределения. Они существенно зависят от порядка расположения уровней во времени. Показатель 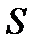 применяется для обнаруживания тенденций изменения дисперсии,
применяется для обнаруживания тенденций изменения дисперсии, 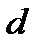 – для обнаруживания тенденций в средней. После того как для исследования ряда найдены фактические значения
– для обнаруживания тенденций в средней. После того как для исследования ряда найдены фактические значения 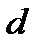 и
и 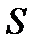 , проверяется гипотеза о том, можно ли считать случайными разности
, проверяется гипотеза о том, можно ли считать случайными разности 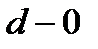 и
и 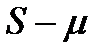 . Гипотезы можно проверить, применяя t-критерий Стьюдента, т.е.
. Гипотезы можно проверить, применяя t-критерий Стьюдента, т.е.
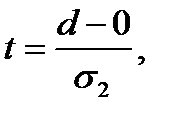 (2.7)
(2.7)
 (2.8)
(2.8)
где  – математическое ожидание величины
– математическое ожидание величины 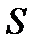 , определенное для случайного расположения уровней во времени;
, определенное для случайного расположения уровней во времени;
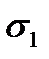 – средняя квадратическая ошибка величины
– средняя квадратическая ошибка величины 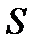 ;
;
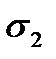 – средняя квадратическая ошибка величины
– средняя квадратическая ошибка величины 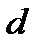 .
.
Необходимые для такой проверки средние квадратические ошибки равны[6]:
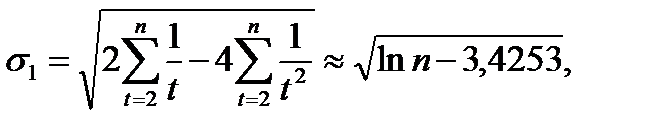 (2.9)
(2.9)
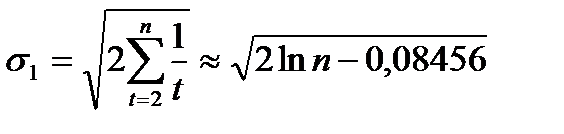 . (2.10)
. (2.10)
Значения  ,
, 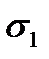 и
и 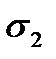 табулированы.
табулированы.
Таблица 2.1
Значение средней  и стандартных ошибок
и стандартных ошибок 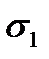 ,
, 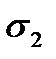 для
для  от 10 до 100 [7]
от 10 до 100 [7]
|
|
|

| 
| 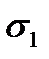
| 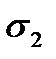
|
| А | |||
| 3,858 | 1,288 | 1,964 | |
| 4,636 | 1,521 | 2,153 | |
| 5,195 | 1,677 | 2,279 | |
| 5,632 | 1,791 | 2,373 | |
| 5,990 | 1,882 | 2,447 | |
| 6,294 | 1,956 | 2,509 | |
| 6,557 | 2,019 | 2,561 | |
| 6,790 | 2,072 | 2,606 | |
| 6,998 | 2,121 | 2,645 | |
| 7,187 | 2,163 | 2,681 | |
| 7,360 | 2,201 | 2,713 | |
| 7,519 | 2,236 | 2,742 | |
| 7,666 | 2,268 | 2,769 | |
| 7,803 | 2,297 | 2,793 | |
| 7,931 | 2,324 | 2,816 | |
| 8,051 | 2,349 | 2,837 | |
| 8,165 | 2,373 | 2,857 | |
| 8,273 | 2,395 | 2,876 | |
| 8,375 | 2,416 | 2,894 |
|
|
|


