 |
Оценка адекватности и точности выбранных моделей
|
|
|
|
Проверка адекватности выбранных моделей реальному процессу строится на анализе случайной компоненты. Ряд остатков получают как отклонения фактических уровней ВР (
) от выровненных (
): 
.
Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения.
Если вид функции выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой, т.е. будет иметь место автокорреляция ошибок. Существует несколько приемов обнаружения автокорреляции. Наиболее распространенный – критерий Дарбина – Уотсона (позволяет обнаружить автокорреляцию первого порядка):
, (2.12)
где 
- коэффициент автокорреляции первого порядка.
Если в ряду остатков имеется сильная положительная автокорреляция, то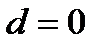 
, в случае сильной отрицательной автокорреляции 
. При отсутствии автокорреляции 
. Применение на практике критерия Дарбина – Уотсона основано на сравнении величины 
с теоретическими табулированными значениями 
и 
:
1. если 
, то гипотеза (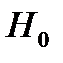
) о независимости случайных отклонений отвергается (отсутствие автокорреляции);
2. если 
, то гипотеза (
) не отвергается;
3. если 
, то нет достаточных оснований для принятия решений (область неопределенности).
Когда расчетное значение превышает 2, то с и сравнивается не сам коэффициент , а (
).
Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности:
1. абсолютная ошибка прогноза:
; (2.13)
2. относительная ошибка прогноза:
|
|
|
(2.14)
3. средняя абсолютная ошибка по модулю:
; (2.15)
4. средняя относительная ошибка по модулю:
(2.16)
Если 
, это свидетельствует о высокой точности модели, при 
- точность хорошая, при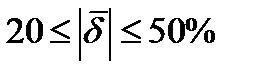 
- удовлетворительная.
5. дисперсия или среднеквадратическая ошибка прогноза (применяется при сравнительной характеристике моделей):
(2.17)
. (2.18)
Чем меньше значение этих характеристик, тем выше точность моделей.
Вопросы для самоконтроля:
1 В чем суть метода Фостера-Стюарта?
2 Назовите критерий для обнаружения автокорреляции.
3 Какие важнейшие характеристики качества модели, выбранной для прогнозирования, вы знаете?
4 На какие 3 класса условно разделяют кривые роста?
Глава 3
_________________________________________________________________
Свойства и оценка параметров основных видов тренда _________________________________________________________________
3.1. Прямолинейный тренд и его свойства.
3.2. Параболический тренд и его свойства.
3.3. Экспоненциальный тренд и его свойства.
Прямолинейный тренд
Самым простым типом линии тренда является прямая линия, описываемая линейным (т.е. первой степени) уравнением тренда: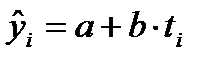 
, где 
- выравненные, то есть лишенные колебаний уровни тренда для лет с № 
, 
– свободный член уравнения, численно равный среднему выравненному уровню для момента или периода времени, принятого за начало отсчета, то есть для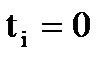 
; 
– средняя величина изменения уровней ряда за единицу изменения времени 
; 
- номера моментов или периодов времени, к которым относятся уровни временного ряда (годы, кварталы, месяцы, даты).
Основные свойства тренда в форме прямой линии таковы:
1. Равные изменения за равные промежутки времени.
2. Если средний абсолютный прирост – положительная величина, то относительные приросты или темпы прироста – постепенно уменьшаются.
3. Если среднее абсолютное изменение – отрицательная величина, то относительные изменения или темпы сокращения постепенно увеличиваются по абсолютной величине снижения к предыдущему уровню.
|
|
|
4. Если тенденция – к сокращению уровней, а изучаемая величина является по определению положительной, то среднее изменение () не может быть больше среднего уровня ().
5. При линейном тренде ускорение, т. е. разность абсолютных изменений за последовательные периоды, равно нулю.
|
|
|
