 |
Модели скользящего среднего.
|
|
|
|
Модель скользящего среднего предполагает, что в ошибках модели в предшествующие периоды сосредоточена информация обо всей предыстории ряда. В этой модели каждое новое значение – среднее между текущей флуктуацией и несколькими (в частности, одной) предыдущими ошибками.
Процесс скользящего среднего порядка q, обозначаемые MA(q) имеют вид:
, (7.16)
где 
- «белый шум» (импульс, шок) с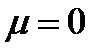 
.
В моделях скользящего среднего для обеспечения стационарности ряда не требуется накладывать никаких ограничений на параметры 
. Однако, если в модели MA (1) параметр 
, то текущее значение 
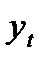будет зависеть от своих прошлых значений берущихся с весами, бесконечно растущими по мере удаления в прошлое:
(7.17)
Чтобы избежать этого, надо, чтобы веса образовывали сходящийся ряд, т.е. 
.
Широко распространены в статистической практике модели скользящего среднего 1-го и 2-го порядка:
MA (1): 
(7.18)
MA (2): 
. (7.19)
Авторегрессионные модели со скользящими средними в остатках.
На практике в целях экономичного описания анализируемого процесса в модель могут быть включены как члены, описывающие Авторегрессионные составляющие, так и члены, моделирующие остаток в виде процесса скользящих средних. Такой процесс называется процессом авторегрессии скользящего среднего – ARMA (p,q):
(7.20)
или
(7.21)
Здесь единственное слагаемое ошибки 
AR – процесса заменяется на процесс MA (q).
Такая модель может интерпретироваться как линейная модель множественной регрессии, в которой в качестве объясняющих переменных выступают прошлые значения самой зависимой переменной, а в качестве регрессионного остатка – скользящие средние из элементов белого шума.
|
|
|
Стационарность процесса ARMA обеспечивается условием 
, а обратимость, в свою очередь гарантируется выполнением условия 
.
Одним из наиболее важных этапов построения моделей стационарных временных рядов является определение ее порядка. Предварительная оценка производится на основе экономического анализа. Чрезмерное повышение порядка модели может и не повысить ее точность. Одновременно расчет большего числа коэффициентов модели при неизменной выборке снижает достоверность оценки каждого из коэффициентов. В то же время недостаточное число коэффициентов модели не позволяет отразить в должной мере динамику процесса и оценить его дальнейшие изменения.
Для определения порядка процесса модели исследуются такие характеристики, как автокорреляционная функция и частная автокорреляционная функция.
На практике, как правило, используют следующие виды моделей, идентифицировать которые можно с помощью анализа АКФ и ЧАКФ (табл. 1.5)[23].
Таблица 7.1
Свойства АКФ и ЧАКФ
| Функция | ARMA (1,0) | ARMA (2,0) | ARMA (0,1) | ARMA (0,2) | ARMA (1,1) |
| АКФ | Экспоненциально затухает (монотонно или знакопеременно) | Экспоненциально затухает или имеет форму синусоидальной волны | Выброс (пик) на лаге 1 | Выбросы (пики) на лагах 1,2 | Экспоненциально затухает от значения  (монотонно или знакопеременно)
|
| ЧАКФ | Выброс (пик) на лаге 1 | Выбросы (пики) на лагах 1,2 | Экспоненциально затухает (монотонно или знакопеременно) | Экспоненциально затухает или имеет форму синусоидальной волны | Экспоненциально затухает от значения 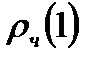 (монотонно или знакопеременно)
|
ARMА- процессы имеют более сложную структуру по сравнению со схожими по поведению AR- или MA- процессами в чистом виде, но при этом ARMA- процессы характеризуются меньшим количеством параметров, что является одним из их преимуществ.
|
|
|
